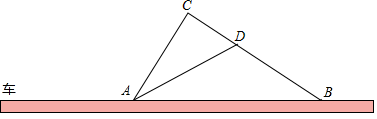
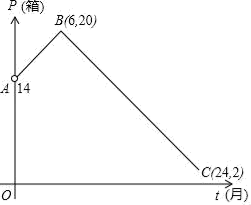
B .
B .  C .
C .  D .
D . 
| a |
![]()

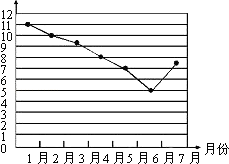
a.甲校20名学生成绩的频数分布表和频数分布直方图如图:
甲校学生样本成绩频数分布表(表1)
|
成绩m(分) |
频数(人数) |
频率 |
|
50≤m<60 |
a |
0.05 |
|
60≤m<70 |
b |
c |
|
70≤m<80 |
3 |
0.15 |
|
80≤m<90 |
8 |
0.40 |
|
90≤m<100 |
6 |
0.30 |
|
合计 |
20 |
1.0 |
b.甲校成绩在80≤m<90的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如表所示(表2):
|
学校 |
平均分 |
中位数 |
众数 |
方差 |
|
甲 |
84 |
n |
89 |
129.7 |
|
乙 |
84.2 |
85 |
85 |
138.6 |

根据以如图表提供的信息,解答下列问题: