①若 ,
,则
;
②若 ,
,且
,则
;
③若 ,
,
,
,则
;
④若 ,
,且
,
,则
.
其中所有正确命题的序号为.
|
乘坐站数 | | | |
| 票价(元) | 3 | 6 | 9 |
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过30站,甲、乙乘坐不超过10站的概率分别为 ,
;甲、乙乘坐超过20站的概率分别为
,
.
(Ⅰ)求甲、乙两人付费相同的概率;
(Ⅱ)设甲、乙两人所付费用之和为随机变量 ,求
的分布列和数学期望.
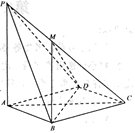
(Ⅰ)求证:直线 平面
;
(Ⅱ)求直线 与平面
所成角的正切值;
(Ⅲ)设点 在线段
上,且二面角
的余弦值为
,求点
到底面
的距离.
(Ⅰ)求椭圆 的方程;
(Ⅱ)是否存在直线 ,使得
,若存在,求出直线
的方程;若不存在,说明理由;
(Ⅲ)设点 是一个动点,若直线
的斜率存在,且
为
中点,
,求实数
的取值范围.