 B .
B .  C .
C . 月用水量(吨) | 4 | 5 | 6 | 9 |
户数 | 3 | 4 | 2 | 1 |

 B .
B .  C .
C .  D .
D . 
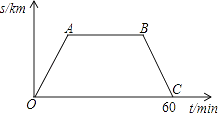
在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象.下列说法错误的是( )

|
捐书(本) |
3 |
4 |
5 |
7 |
10 |
|
人数 |
5 |
7 |
10 |
11 |
7 |
该班学生平均每人捐书本.


88 92 95 99 85 91 86 92 100 95 94 94 88 94 95 97 82 100 99 94 |
整理数据:
| | | |
1 | 4 | a | 8 |
分析数据:
平均数 | 中位数 | 众数 |
93 | b | 94 |
根据以上信息,解答下列问题:
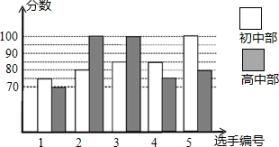
| 平均分 | 中位数 | 众数 | 方差( |
初中部 | | | | |
高中部 | | | | |
①假设此次购进甲种盲盒的个数为a(个),售完这两批盲盒所获总利润为w(元),请写出w与a之间的函数关系式;
②商家如何安排第二批进货方案,才能使售完这两批盲盒获得总利润最大?最大利润是多少元?