河南省新乡市2020年数学中考模拟试卷

更新时间：2024-11-06 浏览次数：278 类型：中考模拟

一、选择题

1. (2024九下·郑州模拟) 下列各数中最小的是（）

A . ﹣5 B . $\text{[math]}$ C . 0 D . ﹣π

答案解析收藏纠错 + 选题
2. (2023七上·五华期中) 根据国家气象局统计，全球平均每年发生雷电次数约为16000000次，将16000000用科学记数法表示为（）

A . 1.6×10⁸ B . 1.6×10⁷ C . 16×10⁶ D . 1.6×10⁶

答案解析收藏纠错 + 选题
3. (2020·新乡模拟) 如图是某几何体的三视图，则该几何体的全面积等于（）

A . 112 B . 136 C . 124 D . 84

答案解析收藏纠错 + 选题
4. (2022八下·雨花期末) 如图是根据某班40名同学一周的体育锻炼情况绘制的统计图，该班40名同学一周参加体育锻炼时间的中位数，众数分别是（）

A . 10.5，16 B . 8.5，16 C . 8.5，8 D . 9，8

答案解析收藏纠错 + 选题
5. (2020·新乡模拟) 一元二次方程x²﹣2kx+k²﹣k+2＝0有两个不相等的实数根，则k的取值范围是（）

A . k＞﹣2 B . k＜﹣2 C . k＜2 D . k＞2

答案解析收藏纠错 + 选题
6. (2021九上·梅里斯期末) 有三张正面分别写有数字﹣2，1，3的卡片，它们背面完全相同，现将这三张卡片背面朝上洗匀后随机抽取一张，以其正面数字作为a的值，然后把这张放回去，再从三张卡片中随机抽一张，以其正面的数字作为b的值，则点（a，b）在第一象限的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·垦利模拟) 若将函数y＝2x²的图象向右平行移动1个单位，再向上平移3个单位，得到的抛物线是（）

A . y＝2（x+5）²﹣1 B . y＝2（x+5）²+1 C . y＝2（x﹣1）²+3 D . y＝2（x+1）²﹣3

答案解析收藏纠错 + 选题
8. (2020·新乡模拟) 如图，△ABC中，∠BAC＝90°，AB＝5，AC＝10，分别以点B和点C为圆心，大于 $\text{[math]}$ BC的长为半径作弧，两弧相交于D、E两点，连接DE交BC于点H，连接AH，则AH的长为（）

A . 5 B . 5 $\text{[math]}$ C . $\text{[math]}$ D . 5 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020·新乡模拟) 如图，在▱ABCO中，A（1，2），B（5，2），将▱ABCO绕O点逆时针方向旋转90°到▱A′B′C′O的位置，则点B′的坐标是（）

A . （﹣2，4） B . （﹣2，5） C . （﹣1，5） D . （﹣1，4）

答案解析收藏纠错 + 选题
10. (2020·新乡模拟) 如图， $\text{[math]}$ ， $\text{[math]}$ ，以BC为直径作半圆，圆心为点O；以点C为圆心， $\text{[math]}$ 为半径作 $\text{[math]}$ ，过点O作AC的平行线交两弧于点D、E，则图中阴影部分的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·合肥模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2020·新乡模拟) 如图，函数y＝2x和y＝ax+5的图象相交于A（1.5，3），则不等式2x＞ax+5的解为.

答案解析收藏纠错 + 选题
13. (2022九上·双流期中) 如图，在以O为原点的直角坐标系中，点A，C分别在x轴、y轴的正半轴上，点B在第一象限内，四边形OABC是矩形，反比例函数y＝ $\text{[math]}$ （x＞0）与AB相交于点D，与BC相交于点E，若BE＝4CE，四边形ODBE的面积是8，则k＝.

答案解析收藏纠错 + 选题
14. (2020·新乡模拟) 如图，在正方形ABCD中， $\text{[math]}$ ，E，F分别为BC，AD上的点，过点E，F的直线将正方形ABCD的面积分为相等的两部分，过点A作 $\text{[math]}$ 于点G，连接DG，则线段DG的最小值为.

答案解析收藏纠错 + 选题
15. (2020九上·闵行期末) 如图，在等腰△ABC中，AB=AC=4，BC=6点D在底边BC上，且∠DAC=∠ACD，将△ACD沿着AD所在直线翻折，使得点C落到点E处，联结BE，那么BE的长为.

答案解析收藏纠错 + 选题

三、解答题

16. (2024九下·苍溪模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ 满足 $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2020·新乡模拟) 为了传承中华优秀传统文化，某校组织八年级学生参加了“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况，随机抽取了其中若干名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，绘制如下不完整的条形统计图.
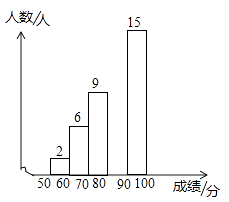
汉字听写大赛成绩分数段统计表
分数段
频数
$\text{[math]}$
2
$\text{[math]}$
6
$\text{[math]}$
9
$\text{[math]}$
18
$\text{[math]}$
15
汉字听写大赛成绩分数段条形统计图
1. （1）补全条形统计图.
2. （2）这次抽取的学生成绩的中位数在的分数段中；这次抽取的学生成绩在 $\text{[math]}$ 的分数段的人数占抽取人数的百分比是.
3. （3）若该校八年级一共有学生350名，成绩在90分以上（含90分）为“优”，则八年级参加这次比赛的学生中成绩“优”等的约有多少人？
答案解析收藏纠错 + 选题
18. (2020·新乡模拟) 已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BD于点F，交⊙O于点D，AC与BD交于点G，点E为OC的延长线上一点，且∠OEB＝∠ACD.
1. （1）求证：BE是⊙O的切线；
2. （2）求证：CD²＝CG•CA；
3. （3）若⊙O的半径为 $\text{[math]}$ ，BG的长为 $\text{[math]}$ ，求tan∠CAB.
答案解析收藏纠错 + 选题
19. (2020·新乡模拟) 如图是某路灯在铅垂面内的示意图，灯柱BC的高为10米，灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩，在地面上的照射区域DE的长为13.3米，从D、E两处测得路灯A的仰角分别为α和45°，且tanα＝6.求灯杆AB的长度.

答案解析收藏纠错 + 选题
20. (2020·新乡模拟) 某校计划一次性购买排球和篮球，每个篮球的价格比排球贵30元，购买2个排球和3个篮球共需340元．
1. （1）求每个排球和篮球的价格；
2. （2）若该校一次性购买排球和篮球共60个，总费用不超过3 800元，且购买排球的个数少于39个，设排球的个数为m，总费用为y元．
  ①求y关于m的函数关系式，并求m可取的所有值；
  
  ②在学校按怎样的方案购买时，费用最低？最低费用为多少？
答案解析收藏纠错 + 选题

21. (2020·新乡模拟) 某“兴趣小组”根据学习函数的经验，对函数y=x+ $\text{[math]}$ 的图象和性质进行了探究，探究过程如下，请补充完整。

（1）函数y=x+ $\text{[math]}$ 的自变量取值范围是；

（2）下表是x与y的几组对应值：

…

-3

-2

-1

- $\text{[math]}$

$\text{[math]}$

…

- $\text{[math]}$

-2

- $\text{[math]}$

$\text{[math]}$

…

则表中m的值为；

（3）根据表中数据，在如图所示平面直角坐标xOy中描点，并画出函数的一部分，请画出
（4）观察函数图象：写出该函数的一条性质
（5）进一步探究发现：函数y=x+ $\text{[math]}$ 图象与直线y=-2只有一交点，所以方程x+ $\text{[math]}$ =-2只有1个实数根，若方程x+ $\text{[math]}$ =k（x<0）有两个不相等的实数根，则k的取值范围是。

答案解析收藏纠错 + 选题

22. (2020·绍兴模拟) 如图，在正方形ABCD中，M、N分别是射线CB和射线DC上的动点，且始终∠MAN＝45°．
1. （1）如图1，当点M、N分别在线段BC、DC上时，请直接写出线段BM、MN、DN之间的数量关系；
2. （2）如图2，当点M、N分别在CB、DC的延长线上时，（1）中的结论是否仍然成立，若成立，给予证明，若不成立，写出正确的结论，并证明；
3. （3）如图3，当点M、N分别在CB、DC的延长线上时，若CN＝CD＝6，设BD与AM的延长线交于点P，交AN于Q，直接写出AQ、AP的长．
答案解析收藏纠错 + 选题
23. (2020·铁岭模拟) 如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线y＝﹣ $\text{[math]}$ x²+bx+c经过点A、C，与AB交于点D．
1. （1）求抛物线的函数解析式；
2. （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．
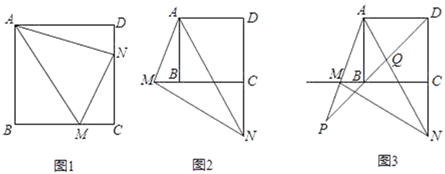
  ①求S关于m的函数表达式；
  
  ②当S最大时，在抛物线y＝﹣ $\text{[math]}$ x²+bx+c的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省新乡市2020年数学中考模拟试卷

副标题：

*注意事项：

河南省新乡市2020年数学中考模拟试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

分数段	频数
$\text{[math]}$	2
$\text{[math]}$	6
$\text{[math]}$	9
$\text{[math]}$	18
$\text{[math]}$	15