河南省禹州市2020年数学中考二模试卷

更新时间：2024-07-13 浏览次数：336 类型：中考模拟

一、选择题

1. (2020·禹州模拟) 在0， $\text{[math]}$ ，-1，2中，最小的数是（）

A . 0 B . -1 C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·禹州模拟) 国务院印发《“十三五”国家信息化规划》，提出到2020年信息产业收入规模预计达到26.2万亿元.将数据“26.2万亿”用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·禹州模拟) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·苏州模拟) 受新型冠状病毒肺炎影响，学校开学时间延迟，为了保证学生停课不停学，某校开始实施网上教学，张老师统计了本班学生一周网上上课的时间（单位：分钟）如下：200，180，150，200，250.关于这组数据，下列说法正确的是（）

A . 中位数是200 B . 众数是150 C . 平均数是190 D . 方差为0

答案解析收藏纠错 + 选题
5. (2020·禹州模拟) 一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
6. (2020·禹州模拟) 解分式方程 $\text{[math]}$ ，去分母得（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·河南模拟) 如图， $\text{[math]}$ 的对角线AC与BD相交于点O，且∠OCD=90°.若E是BC边的中点，BD=10，AC=6，则OE的长为（）

A . 1.5 B . 2 C . 2.5 D . 3

答案解析收藏纠错 + 选题
8. (2020·禹州模拟) 已知某二次函数的图象与 $\text{[math]}$ 轴相交于A，B两点.若该二次函数图象的对称轴是直线 $\text{[math]}$ ，且点A的坐标是 $\text{[math]}$ ，则AB的长为（）

A . 5 B . 8 C . 10 D . 11

答案解析收藏纠错 + 选题
9. (2020·禹州模拟) 如图，在 $\text{[math]}$ 中，以点A为圆心，AC的长为半径作弧，与BC交于点E，分别以点E，C为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点P，作射线AP交BC于点D.若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020·禹州模拟) 如图，矩形ABCD的周长是28cm，且AB比BC长2cm.若点P从点A出发，
以1cm/s的速度沿A→D→C方向匀速运动，同时点Q从点A出发，以2cm/s的

速度沿A→B-→C方向匀速运动，当一个点到达点C时，另一个点也随之停止运动.若

设运动时间为t(s)， $\text{[math]}$ 的面积为S(cm2)，则s(cm2)与t(s)之间的函数图象大致

是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2024九上·开州期中) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2020·泗水模拟) 不等式组 $\text{[math]}$ 的整数解是.

答案解析收藏纠错 + 选题
13. (2020·绍兴模拟) 现有形状大小一样、背面相同的五张卡片，在它们的正面分别标有数字0，1，2，3，6.若把五张卡片背面朝上，洗匀放在桌子上，然后任意抽取一张卡片，不放回，再任意抽取一张卡片，则抽取的两张卡片上的数字的积不大于2的概率是.

答案解析收藏纠错 + 选题
14. (2020·禹州模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，则图中阴影部分的面积是.

答案解析收藏纠错 + 选题
15. (2020·禹州模拟) 如图，AC是 $\text{[math]}$ 的对角线，∠BAC =90°， $\text{[math]}$ 的边AB，AC，BC的长是三个连续偶数，E，F分别是边AB，BC上的动点，且EF⊥BC，将s BEF沿着EF折叠得到 $\text{[math]}$ ，连接AP，DP.若△APD为直角三角形时，BF 的长为.

答案解析收藏纠错 + 选题

三、解答题

16. (2020·禹州模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2020·禹州模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以点A为圆心，AC的长为半径作OA，交AB于点D，交CA的延长线于点E.过点E作EF//AB，交OA于点F，连接AF，BF，DF.
1. （1）求证：BF是 $\text{[math]}$ 的切线；
2. （2）填空：
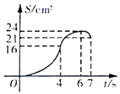
  ①当四边形ADFE是周长为20的菱形时，BF=；
  
  ②当 $\text{[math]}$ 时，四边形ACBF是正方形.
答案解析收藏纠错 + 选题

18. (2020·禹州模拟) 2019年10月1日是新中国成立70周年.某学校国庆节后，为了调查学生对这场阅兵仪式的关注情况，在全校组织了一次全体学生都参加的“阅兵仪式有关知识”的考试，批改试卷后，学校政教处随机抽取了部分学生的考卷进行成绩统计，发现成绩最低是51分，最高是100分，根据统计结果，绘制了如下尚不完整的统计图表.

调查结果频数分布表

分数段/分	频数	频率
$\text{[math]}$	$\text{[math]}$	0.1
$\text{[math]}$	18	0.18
$\text{[math]}$	$\text{[math]}$	0.25
$\text{[math]}$	35	$\text{[math]}$
$\text{[math]}$	12	0.12

请根据以上信息，解答下列问题：

（1） $\text{[math]}$ ；
（2）若把上面频数分布表中的信息画在扇形统计图内，则 $\text{[math]}$ 所在扇形圆心角的度数是；
（3）请将频数分布直方图补充完整；
（4）若该校有1200名学生，请估计该校分数x在 $\text{[math]}$ 范围的学生有多少名.

答案解析收藏纠错 + 选题

19. (2020·禹州模拟) 清代《修武县志》有胜果寺的记载，“康熙五十二年三月十七日，塔顶现青白二气
如云，越二日乃止”，此文中的塔即为“胜果寺塔”，是修武作为“千年古县”的标志性古建筑.为了测量塔的高度，某校数学兴趣小组的两名同学采用了如下方式进行测量.如

图，小明站在A处，眼睛E距离地面的高度为1.85m，测得塔顶C的仰角为45°，小

红站在距离小明10m的D处，眼睛F距离地面的高度为1.5m，测得塔顶C的仰角为

60°，已知4，D，塔底B在同一水平面上，由此即可求出塔高BC .你知道是怎么求的吗？请写出解题过程.（结果精确到 $\text{[math]}$ .参考数据： $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2020·禹州模拟) 如图，在平面直角坐标系中，点A的坐标为 $\text{[math]}$ ，点B在y轴正半轴上，且 $\text{[math]}$ ，以AB为边在第一象限内作正方形ABCD，且双曲线 $\text{[math]}$ 经过点D.
1. （1）求k的值；
2. （2）将正方形 $\text{[math]}$ 沿 $\text{[math]}$ 轴负方向平移得到正方形 $\text{[math]}$ ，当点 $\text{[math]}$ 恰好落在双曲线 $\text{[math]}$ 上时，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
21. (2021·北部湾模拟) 河南灵宝苹果为中华苹果之翘楚，被誉为“中华名果”.某水果超市计划从灵宝购进“红富士”与“新红星”两种品种的苹果.已知2箱红富士苹果的进价与3箱新红星苹果的进价的和为282元，且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元.
1. （1）求每箱红富士苹果的进价与每箱新红星苹果的进价分别是多少元？
2. （2）如果购进红富士苹果有优惠，优惠方案是：购进红富士苹果超过20箱，超出部分可以享受七折优惠.若购进 $\text{[math]}$ （ $\text{[math]}$ ，且 $\text{[math]}$ 为整数）箱红富士苹果需要花费 $\text{[math]}$ 元，求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
3. （3）在（2）的条件下，超市决定在红富士、新红星两种苹果中选购其中一种，且数量超过20箱，请你帮助超市选择购进哪种苹果更省钱.
答案解析收藏纠错 + 选题
22. (2020·禹州模拟) 如图
1. （1）问题发现
  如图1， $\text{[math]}$ 是等边三角形，点D，E分别在边BC， $\text{[math]}$ 上.若 $\text{[math]}$ ，则AB，CE，BD，DC之间的数量关系是；
2. （2）拓展探究
  如图2， $\text{[math]}$ 是等腰三角形， $\text{[math]}$ ， $\text{[math]}$ ，点D，E分别在边BC，AC上.若 $\text{[math]}$ ，则（1）中的结论是否仍然成立？请说明理由.
3. （3）解决问题
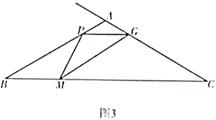
  如图3，在 $\text{[math]}$ 中，∠B=30°， AB= AC =4cm，点P从点A出发，以1cm/s的
  
  速度沿A→B方向匀速运动，同时点M从点B出发，以√↓3cm/s的速度沿B→C方
  
  向匀速运动，当其中一个点运动至终点时，另一个点随之停止运动.连接PM，在PM
  
  右侧作∠PMG= 30°，该角的另一边交射线CA于点G，连接PG .设运动时间为t(s)，
  
  当 $\text{[math]}$ 为等腰三角形时，直接写出t的值.
答案解析收藏纠错 + 选题
23. (2020·唐河模拟) 如图，若抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴相交于A，B两点，与y轴相交于点C，直线 $\text{[math]}$ 经过点B，C.
1. （1）求抛物线的解析式；
2. （2）点P是直线BC下方抛物线上一动点，过点P作 $\text{[math]}$ 轴于点H，交BC于点M，连接PC.
  ①线段PM是否有最大值？如果有，求出最大值；如果没有，请说明理由；
  
  ②在点P运动的过程中，是否存在点M，恰好使 $\text{[math]}$ 是以PM为腰的等腰三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由.
答案解析收藏纠错 + 选题