北京市丰台区2018-2019学年八年级下学期数学期末考试试...

更新时间：2021-05-20 浏览次数：251 类型：期末考试

一、选择题

1. (2021九上·大兴期中) 下列图书馆的标志中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八下·赫山期末) 下面的多边形中，内角和与外角和相等的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021九上·北京开学考) 一元二次方程 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九上·北京开学考) 如图，矩形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 交于点 $\text{[math]}$ ，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021九上·北京开学考) 周长为 $\text{[math]}$ 的正方形对角线的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020七下·海淀月考) 下图是北京世界园艺博览会园内部分场馆的分布示意图，在图中，分别以正东、正北方向为 $\text{[math]}$ 轴、 $\text{[math]}$ 轴的正方向建立平向直角坐标系，如果表示演艺中心的点的坐标为 $\text{[math]}$ ，表示水宁阁的点的坐标为 $\text{[math]}$ ，那么下列各场馆的坐标表示正确的是（）

A . 中国馆的坐标为 $\text{[math]}$ B . 国际馆的坐标为 $\text{[math]}$ C . 生活体验馆的坐标为 $\text{[math]}$ D . 植物馆的坐标为 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2019八下·北京期末) 为了迎接2022年的冬奥会，中小学都积极开展冰上运动，小明和小刚进行 $\text{[math]}$ 米短道速滑训练，他们的五次成绩如下表所示：

设两个人的五次成绩的平均数依次为 $\text{[math]}$ 、 $\text{[math]}$ ，方差依次为 $\text{[math]}$ 、 $\text{[math]}$ ，则下列判断正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·北京开学考) 在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图像互相平行，如果这两个函数的部分自变量和对应的函数值如下表所示：

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

那么 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2020·如皋模拟) 函数y= $\text{[math]}$ 中，自变量x的取值范围是；实数2﹣ $\text{[math]}$ 的倒数是．

答案解析收藏纠错 + 选题
10. (2019八下·北京期末) 如图，菱形ABCD的对角线交于点O、E为AD边的中点，如果菱形的周长为 $\text{[math]}$ ，那么OE的长是．

答案解析收藏纠错 + 选题
11. (2019八下·北京期末) 公元9世纪，阿拉伯数学家阿尔•花拉子米在他的名著《代数学》中用图解一元二次方程，他把一元二次方程 $\text{[math]}$ 写成 $\text{[math]}$ 的形式，并将方程左边的 $\text{[math]}$ 看作是由一个正方形(边长为 $\text{[math]}$ )和两个同样的矩形(一边长为 $\text{[math]}$ ，另一边长为 $\text{[math]}$ )构成的矩尺形，它的面积为 $\text{[math]}$ ，如图所示。于是只要在这个图形上添加一个小正方形，即可得到一个完整的大正方形，这个大正方形的面积可以表小为： $\text{[math]}$ $\text{[math]}$ ，整理，得 $\text{[math]}$ ，因为 $\text{[math]}$ 表示边长，所以 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2021八下·阿荣旗期末) 如图，在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，则关于 $\text{[math]}$ 的二元一次方程组 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
13. (2024九上·江阴期中) 已知矩形 $\text{[math]}$ ，给出三个关系式：① $\text{[math]}$ ② $\text{[math]}$ ③ $\text{[math]}$ 如果选择关系式作为条件（写出一个即可），那么可以判定矩形为正方形，理由是 .

答案解析收藏纠错 + 选题
14. (2019八下·北京期末) 体育张教师为了解本校八年级女生：“1分钟仰卧起坐”的达标情况，随机抽取了20名女生进行仰卧起坐测试．如图是根据测试结果绘制的频数分布直方图．如果这组数据的中位数是40次，那么仰卧起坐次数为40次的女生人数至少有人．

答案解析收藏纠错 + 选题
15. (2021九上·北京开学考) 在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ，如果以 $\text{[math]}$ 为顶点的四边形是平行四边形，那么满足条件的所有点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题

三、综合题

16. (2019八下·北京期末) 甲、乙两个车间接到加工一批零件的任务，从开始加工到完成这项任务共用了9天．其间，乙车间在加工2天后停止加工，引入新设备后继续加工，直到与甲车间同时完成这项任务为止，设甲、乙两个车间各自加工零件总数y（单位：件）与加时间x（单位：天）的对应关系如图1所示，由工厂统计数据可知，甲车间与乙车间加工零件总数之差z（单位：件）与加时间x（单位：天）的对应关系如图2所示，请根据图象提供的信息回答：
1. （1）图中 $\text{[math]}$ 的值是；
2. （2）第天时，甲、乙两个车间加工零件总数相同.
答案解析收藏纠错 + 选题
17. (2021九上·海州期末) 解方程：x²﹣6x+8＝0．

答案解析收藏纠错 + 选题
18. (2020九上·北京月考) 下面是小东设计的“作矩形”的尺规作图过程，已知： $\text{[math]}$
求作：矩形 $\text{[math]}$

作法：如图，

①作线段 $\text{[math]}$ 的垂直平分线角交 $\text{[math]}$ 于点 $\text{[math]}$ ；

②连接 $\text{[math]}$ 并延长，在延长线上截取 $\text{[math]}$

③连接 $\text{[math]}$

所以四边形 $\text{[math]}$ 即为所求作的矩形

根据小东设计的尺规作图过程
1. （1）使用直尺和圆规，补全图形：（保留作图痕迹）
2. （2）完成下边的证明：
  证明： $\text{[math]}$ ， $\text{[math]}$ ，
  
  $\text{[math]}$ 四边形是平行四边形（）（填推理的依据）
  
  $\text{[math]}$
  
  $\text{[math]}$ 四边形 $\text{[math]}$ 是矩形（）（填推理的依据）
答案解析收藏纠错 + 选题
19. (2022八下·房山期中) 在平面直角坐标系 $\text{[math]}$ 中，已知一次函数 $\text{[math]}$ 的图像与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$
1. （1）求 $\text{[math]}$ 两点的坐标
2. （2）在给定的平面直角坐标系中画出该函数的图象；
3. （3）根据图像回答：当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是.
答案解析收藏纠错 + 选题
20. (2019八下·北京期末) 如图，▱ABCD中，E ， F为对角线AC上的两点，且BE∥DF；求证：AE=CF ．

答案解析收藏纠错 + 选题
21. (2019八下·北京期末) 关于x的一元二次方程x²-2x+m=0有两个实数根．
1. （1）求m的取值范围；
2. （2）请选择一个合适的数作为m的值，并求此时方程的根．
答案解析收藏纠错 + 选题

22. (2019九上·海淀开学考) 据《北京晚报》介绍，自2009年故宫博物院年度接待观众首次突破1000万人次之后，每年接待量持续增长，到2018年突破1700万人次，成为世界上接待量最多的博物馆．特别是随着《我在故宫修文物》、《上新了，故宫》等一批电视文博节目的播出，社会上再次掀起故宫热．于是故宫文创营销人员为开发针对不同年龄群体的文创产品，随机调查了部分参观故宫的观众的年龄，整理并绘制了如下统计图表．

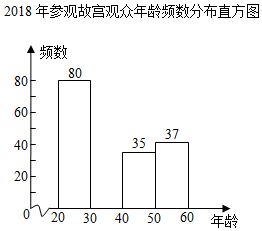
2018年参观故宫观众年龄频数分布表

年龄x/岁	频数/人数	频率
20≤x＜30	80	b
30≤x＜40	a	0.240
40≤x＜50	35	0.175
50≤x＜60	37	c
合计	200	1.000

（1）求表中a ， b ， c的值；
（2）补全频数分布直方图；
（3）从数据上看，年轻观众（20≤x＜40）已经成为参观故宫的主要群体．如果今年参观故宫人数达到2000万人次，那么其中年轻观众预计约有万人次．

答案解析收藏纠错 + 选题

23. (2019八下·北京期末) “美化城市，改善人民居住环境”是城市建设的一项重要内容．北京市将重点围绕城市副中心、大兴国际机场、冬奥会、世园会、永定河、温榆河、南中轴等重要节点区域绿化，到2022年，全市将真正形成一片集“万亩城市森林、百万乔灌树木、百种乡土植物、二十四节气林窗、四季景观大道”于一体的城市森林.2018年当年计划新增造林23万亩，2019年计划新增造林面积大体相当于27.8个奥森公园的面积，预计2020年计划新增造林面积达到38.87万亩，求2018年至2020年计划新增造林面积的年平均增长率．

答案解析收藏纠错 + 选题
24. (2019九上·海淀开学考) 如图， $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点.
1. （1）求证：四边形 $\text{[math]}$ 是菱形
2. （2）如果 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
25. (2021九上·北京开学考) 在平面直角坐标系xOy中，直线y=kx+b（k≠0）与直线y=-x+4的交点为P（3，m），与y轴交于点A ．
1. （1）求m的值；
2. （2）如果△PAO的面积为3，求直线y=kx+b的表达式．
答案解析收藏纠错 + 选题

26. (2019八下·北京期末) 如图，点 $\text{[math]}$ 是菱形 $\text{[math]}$ 边上的一个动点，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 的方向匀速运动到 $\text{[math]}$ 停止，过点 $\text{[math]}$ 作 $\text{[math]}$ 垂直直线 $\text{[math]}$ 于点 $\text{[math]}$ ，已知 $\text{[math]}$ ，设点 $\text{[math]}$ 走过的路程为 $\text{[math]}$ ，点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离为 $\text{[math]}$ （当点 $\text{[math]}$ 与点 $\text{[math]}$ 或点 $\text{[math]}$ 重合时， $\text{[math]}$ 的值为 $\text{[math]}$ ）

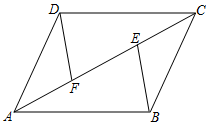
小腾根据学习函数的经验，对函数随自变量的变化规律进行了探究，下面是小腾的探究过程，请补充完整；

（1）按照下表中自变量的值进行取点，画图，测量，分别得到了以下几组对应值；

$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$		$\text{[math]}$	$\text{[math]}$		$\text{[math]}$	$\text{[math]}$

（2）在同一平面直角坐标系 $\text{[math]}$ 中，描出补全后的表中各组数值所对应的点 $\text{[math]}$ ，并画出函数的图象；
（3）结合函数图象，解决问题，当点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离恰为点 $\text{[math]}$ 走过的路程的一半时，点P走过的路程约是 $\text{[math]}$

答案解析收藏纠错 + 选题

27. (2019八下·北京期末) 正方形ABCD中，点M是直线BC上的一个动点（不与点B ， C重合），作射线DM ，过点B作BN⊥DM于点N ，连接CN ．
1. （1）如图1，当点M在BC上时，如果∠CDM=25°，那么∠MBN的度数是．
2. （2）如图2，当点M在BC的延长线上时，
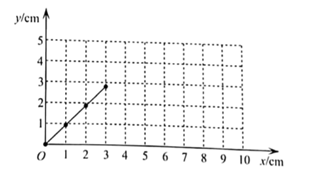
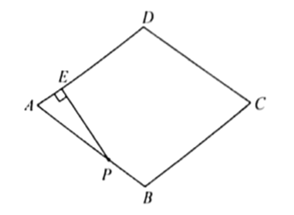
  ①依题意补全图2；
  
  ②用等式表示线段NB ， NC和ND之间的数量关系，并证明．
答案解析收藏纠错 + 选题
28. (2019八下·北京期末) 对于平面直角坐标系xOy中的图形W和点P ，给出如下定义：F为图形W上任意一点，将P ， F两点间距离的最小值记为m ，最大值记为M ，称M与m的差为点P到图形W的“差距离”，记作d（P ， W），即d（P ， W）=M-m ，已知点A（2，1），B（-2，1）
1. （1）求d（O ， AB）；
2. （2）点C为直线y=1上的一个动点，当d（C ， AB）=1时，点C的横坐标是；
3. （3）点D为函数y=x+b（-2≤x≤2）图象上的任意一点，当d（D ， AB）≤2时，直接写出b的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

北京市丰台区2018-2019学年八年级下学期数学期末考试试...

副标题：

*注意事项：

北京市丰台区2018-2019学年八年级下学期数学期末考试试...

试题分析

总体分析

题量分析

难度分析

知识点分析