江苏省无锡市锡山区2019-2020学年八年级下学期数学期中...

更新时间：2024-07-13 浏览次数：248 类型：期中考试

一、选择题

1. (2020八下·锡山期中) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020八下·锡山期中) 若分式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . x≠0 B . x≠－ $\text{[math]}$ C . x≠ $\text{[math]}$ D . x≠2

答案解析收藏纠错 + 选题
3. (2020七上·历城期末) 下列调查方式，你认为最合适的是（）.

A . 日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式； B . 旅客上飞机前的安检，采用抽样调查方式； C . 了解娄底市居民日平均用水量，采用全面调查方式； D . 对2019年央视春节联欢晚会收视率的调查，适合用抽样调查方式.

答案解析收藏纠错 + 选题
4. (2020八下·锡山期中) 下列各事件中，属于必然事件的是（）

A . 抛一枚硬币，正面朝上 B . 早上出门，在第一个路口遇到红灯 C . 在平面内，度量一个三角形的内角度数，其和为360° D . 5本书分放在4个抽屉，至少一个抽屉内有2本书

答案解析收藏纠错 + 选题
5. (2022八下·攸县期末) 数据共40个，分为6组，第1到第四组的频数分别为10，5，7，6，第5组的频率为0.1，则第6组的频数为（）

A . 4 B . 10 C . 6 D . 8

答案解析收藏纠错 + 选题
6. (2020八下·锡山期中) 如果把分式 $\text{[math]}$ 中的x、y都扩大3倍，那么分式的值（）

A . 扩大3倍 B . 不变 C . 缩小3倍 D . 扩大9倍

答案解析收藏纠错 + 选题
7. (2020八上·安丘期末) 某画室分两次购买了相同的素描本，第一次用120元购买了若干本，第二次在同一家商店又购买了240元，这次商家每本优惠4元，结果比上次多买了20本.设第一次买了x本素描本，列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024八下·扬州月考) 下列性质中，矩形具有而菱形不一定具有的是（）

A . 对角线相等 B . 对角线互相平分 C . 对角线互相垂直 D . 邻边相等

答案解析收藏纠错 + 选题
9. (2024八下·德城期中)
如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . 12 D . 24

答案解析收藏纠错 + 选题
10. (2020八下·锡山期中) 如图，矩形ABCD中，AB＝2，对角线AC、BD交于点O，∠AOD＝120°，E为BD上任意点，P为AE中点，则PO＋PB的最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·江阴期中) 当x＝时，分式 $\text{[math]}$ 的值为0.

答案解析收藏纠错 + 选题
12. (2020八下·锡山期中) 某市有16000名学生参加考试，为了了解考试情况，从中抽取1000名学生的成绩进行统计分析，在这个问题中，样本容量是.

答案解析收藏纠错 + 选题
13. (2022八下·南京月考) 某种油菜籽在相同条件下发芽试验的结果如表：
每批粒数n
100
300
400
600
1000
2000
3000
发芽的频数m
96
284
380
571
948
1902
2848
发芽的频率 $\text{[math]}$
0.960
0.947
0.950
0.952
0.948
0.951
0.949
那么这种油菜籽发芽的概率是（结果精确到0.01）．

答案解析收藏纠错 + 选题
14. (2024八下·新昌期中) 在平行四边形ABCD中，若∠A+∠C=100°，则∠D=.

答案解析收藏纠错 + 选题
15. (2020八下·锡山期中) 要使▱ABCD 是菱形，你添加的条件是.（写出一种即可）

答案解析收藏纠错 + 选题
16. (2024八下·苏州工业园月考) 关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有增根，则m＝.

答案解析收藏纠错 + 选题
17. (2020八下·锡山期中) 如图，矩形ABCD的对角线交于点O，点E在线段AO上，且DE＝DC，若∠EDO＝15°，则∠DEC＝°.

答案解析收藏纠错 + 选题
18. (2020八下·锡山期中) E、F是线段AB上的两点，且AB＝16，AE＝1，BF＝3，点G是线段EF上的一动点，分别以AG、BG为斜边在AB同侧作两个等腰直角三角形，直角顶点分别为D、C，如图所示，连接CD并取中点P，连结PG，点G从E点出发运动到F点，则线段PG扫过的图形面积为.

答案解析收藏纠错 + 选题

三、解答题

19. (2020八下·锡山期中) 化简或计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2022八下·长沙开学考) 先化简再求值： $\text{[math]}$ ，其中 $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2020八下·锡山期中) 解下列分式方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
22. (2020八下·锡山期中) 某校为研究学生的课余活动情况，采取抽样的方法，从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制了如下的两幅不完整的统计图（如图），请你根据图中提供的信息解答下列问题：
1. （1）这次调研，一共调查了人.
2. （2）有阅读兴趣的学生占被调查学生总数的%.
3. （3）有“其它”爱好的学生共多少人？
4. （4）补全折线统计图.
答案解析收藏纠错 + 选题
23. (2023八下·大冶期末) 在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．
1. （1）求证：△ABE≌△ADF；
2. （2）试判断四边形AECF的形状，并说明理由．
答案解析收藏纠错 + 选题
24. (2020八下·锡山期中) 只用无刻度的直尺作图（保留作图痕迹，不要求写作法）
1. （1）如图1，已知∠AOB，OA＝OB，点E在OB边上，其中四边形AEBF是平行四边形，请你在图中画出∠AOB的平分线.
2. （2）如图2，已知E是菱形ABCD中AB边上的中点，请你在图中画出一个矩形EFGH，使得其面积等于菱形ABCD的一半.
答案解析收藏纠错 + 选题
25. (2020八下·锡山期中) 阅读下面的材料：
如果函数y＝f(x)满足：对于自变量x的取值范围内的任意x₁ ， x₂ ，

①若 $\text{[math]}$ ，都有 $\text{[math]}$ ，则称f(x)是增函数；

②若 $\text{[math]}$ ，都有 $\text{[math]}$ ，则称f(x)是减函数.

例题：证明函数f(x)＝ $\text{[math]}$ 是减函数.

证明：设 $\text{[math]}$ ，

$\text{[math]}$

∵ $\text{[math]}$ ，

∴ $\text{[math]}$ .

∴ $\text{[math]}$ .即 $\text{[math]}$ .

∴ $\text{[math]}$ .

∴函数 $\text{[math]}$ 是减函数.

根据以上材料，解答下面的问题：

已知函数f(x)＝ $\text{[math]}$ （x＜0），例如f(－1)＝ $\text{[math]}$ ＝－3，f(－2)＝ $\text{[math]}$ ＝－ $\text{[math]}$
1. （1）计算：f(－3)＝；
2. （2）猜想：函数f(x)＝ $\text{[math]}$ （x＜0）是函数（填“增”或“减”）；
3. （3）请仿照例题证明你的猜想.
答案解析收藏纠错 + 选题
26. (2020八下·锡山期中) （发现问题）爱好数学的小强在做作业时碰到这样的一道题目：如图①，在△ABC中，AB＝8，AC＝6，E为BC中点，求AE的取值范围.
1. （1）（解决问题）
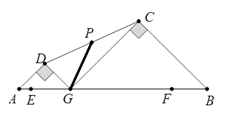
  小强经过多次的尝试与探索，终于得到解题思路：在图①中，作AB边上的中点F，连接EF，构造出△ABC的中位线EF，请你完成余下的求解过程.
2. （2）（灵活运用）
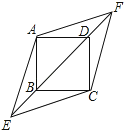
  如图②，在四边形ABCD中，AB＝8，CD＝6，E、F分别为BC、AD中点，求EF的取值范围.
3. （3）变式：把图②中的A、D、C变成在一直线上时，如图③，其它条件不变，则EF的取值范围为.
4. （4）（迁移拓展）
  如图④，在△ABC中，∠A＝60°，AB＝4，E为BC边的中点，F是AC边上一点且EF正好平分△ABC的周长，则EF=.
答案解析收藏纠错 + 选题
27. (2020八下·锡山期中) 如图①，将正方形ABOD放在平面直角坐标系中，O是坐标原点，点D的坐标为（2，3），
1. （1）点B的坐标为；
2. （2）若点P为对角线BD上的动点，作等腰直角三角形APE，使∠PAE＝90°，如图②，连接DE，则BP与DE的关系（位置与数量关系）是▲ ，并说明理由；
3. （3）在（2）的条件下，再作等边三角形APF，连接EF、FD，如图③，在 P点运动过程中当EF取最小值时，此时∠DFE＝°；
4. （4）在（1）的条件下，点 M在 x 轴上，在平面内是否存在点N，使以 B、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题