河北省保定市定兴县2020年中考数学一模试卷

更新时间：2024-11-06 浏览次数：322 类型：中考模拟

一、单选题

1. 如图，一个三角形只剩下一个角，这个三角形为（　　）

A . 锐角三角形 B . 钝角三角形 C . 直角三角形 D . 以上都有可能

答案解析收藏纠错 + 选题
2. (2020七上·栾城期中) 某排球队检测排球，其中质量超过标准的克数记为正数，不足的克数记为负数.下面是检测过的四个排球，在其上方标注了检测结果，其中质量最接近标准的一个是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·定兴模拟) 如图，AB∥CD，∠C=48°，∠1=（　　）

A . 42° B . 48° C . 132° D . 138°

答案解析收藏纠错 + 选题
4. (20212九上·义乌期末) 如图，在由边长相同的7个正六边形组成的网格中，点A，B在格点上．再选择一个格点C，使△ABC是以AB为腰的等腰三角形，符合点C条件的格点个数是（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
5. (2020·定兴模拟) 下列调查：
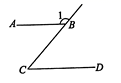
①机场对乘客进行安检；②对北京世园会游客满意度的调查；

③对全省中学生视力情况的调查；④九年级一班要选出1人参加学校的100米比赛．

其中适合全面调查的是（　　）

A . ②③ B . ①④ C . ②④ D . ①③

答案解析收藏纠错 + 选题
6. (2020·定兴模拟) 把0.00205写成a×10ⁿ（1≤a＜10，n为整数）的形式，则n为（　　）

A . －2 B . －3 C . －4 D . －5

答案解析收藏纠错 + 选题
7. (2024八下·高碑店月考) 计算：125²-50×125+25²=（）

A . 100 B . 150 C . 10000 D . 22500

答案解析收藏纠错 + 选题
8. (2020·定兴模拟) 已知二元一次方程组 $\text{[math]}$ ，如果用加减消元法消去y，则下列方法可行的是（　　）

A . ①×4＋②×5 B . ①×5＋②×4 C . ①×5－②×4 D . ①×4－②×5

答案解析收藏纠错 + 选题
9. (2020·新乡模拟) 关于x的方程x²＋2x－a=0没有实数根，则a的值可能是（　　）

A . －2 B . －1 C . 0 D . 2

答案解析收藏纠错 + 选题
10. (2020·定兴模拟) 已知：∠MON，如图，小静进行了以下作图：
①在∠MON的两边上分别截取OA，OB，使OA=OB；

②分别以点A，B为圆心，OA长为半径作弧，两弧交于点C；

③连接AC，BC，AB，OC．

若OC=2，S_四边形_OACB=4，则AB的长为（　　）

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
11. (2020七上·重庆月考) 要制作一个密封的长方体铁盒，嘉嘉设计出了它的三视图，如图，按图中尺寸（单位：cm）判断，要制作这个长方体铁盒，如果只考虑面积因素，采用下列哪种面积的铁板最合理（　　）

A . 1000cm² B . 1030cm² C . 1100cm² D . 1200cm²

答案解析收藏纠错 + 选题
12. (2020·定兴模拟) 如图，函数 $\text{[math]}$ （k≠0，x＜0）的图像L经过点A（－4，2），直线AB与x轴交于点B（－5，0），经过点C（0，4）作y轴的垂线，分别交L和直线AB于点M，N，则MN=（　　）

A . 1 B . －5 C . －1 D . 5

答案解析收藏纠错 + 选题
13. (2020·定兴模拟) 如图，在平整的桌面上面一条直线l，将三边都不相等的三角形纸片ABC平放在桌面上，使AC与边l对齐，此时△ABC的内心是点P；将纸片绕点C顺时针旋转，使点B落在l上的点B'处，点A落在A'处，得到△A'B'C'的内心点P'．下列结论正确的是（　　）

A . PP'与l平行，PC与P'B'平行 B . PP'与l平行，PC与P'B'不平行 C . PP'与l不平行，PC与P'B'平行 D . PP'与l不平行，PC与P'B'不平行

答案解析收藏纠错 + 选题
14. (2020·定兴模拟) 如图，一艘货船在A处，巡逻艇C在其南偏西60°的方向上，此时一艘客船在B处，巡逻艇C在其南偏西20°的方向上，则此时从巡逻艇上看这两艘船的视角 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2020·定兴模拟) 如图，数轴上有两点A，B，表示的数分别是m，n．已知m，n是两个连续的整数，且m＋n=－1，则分式 $\text{[math]}$ ÷ $\text{[math]}$ 的值为（　　）

A . －1 B . 1 C . 3 D . －3

答案解析收藏纠错 + 选题
16. (2020·定兴模拟) 如图，∠ACB=90°，AC=BC，CD平分∠ACB，点D，E关于CB对称，连接EB并延长，与AD的延长线交于点F，连接DE，CE．对于以下结论：
①DE垂直平分CB；②AD=BE；③∠F不一定是直角；④EF²＋DF²=2CD² ．

其中正确的是（　　）

A . ①④ B . ②③ C . ①③ D . ②④

答案解析收藏纠错 + 选题

二、填空题

17. (2020·定兴模拟) $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2020·呼和浩特模拟) 根据如下程序，解决下列问题：
1. （1）当m=－1时，n=；
2. （2）若n=6，则m=．
答案解析收藏纠错 + 选题
19. (2020·定兴模拟) 如图，下列正多边形都满足BA₁=CB₁ ，在正三角形中，我们可推得：∠AOB₁=60°；在正方形中，可推得：∠AOB₁=90°；在正五边形中，可推得：∠AOB₁=108°，依此类推在正八边形中，AOB₁=°，在正n（n≥3）边形中，∠AOB₁=°．

答案解析收藏纠错 + 选题

三、解答题

20. (2020七上·余干月考) 对于四个数“－6，－2，1，4”及四种运算“＋，－，×，÷”，列算式解答：
1. （1）求这四个数的和；
2. （2）在这四个数中选出两个数，填入下列□中，使得：
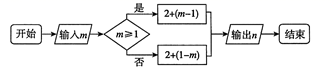
  ①“□－□”的结果最小；
  
  ②“□×□”的结果最大．
3. （3）在这四个数中选出三个数，在四种运算中选出两种，组成一个算式，使运算结果等于没选的那个数．
答案解析收藏纠错 + 选题
21. (2020·定兴模拟) 如图1，给定一个正方形，要通过画线将其分割成若干个互不重叠的正方形．第1次画线分割成4个互不重叠的正方形，得到图2；第2次画线分割成7个互不重叠的正方形，得到图3……以后每次只在上次得到图形的左上角的正方形中画线．
1. （1）尝试：
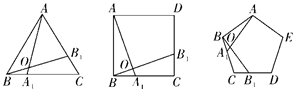
  第3次画线后，分割成个互不重叠的正方形；
  
  第4次画线后，分割成个互不重叠的正方形．
2. （2）发现：第n次画线后，分割成个互不重叠的正方形；并求第2020次画线后得到互不重叠的正方形的个数．
3. （3）探究：若干次画线后，能否得到1001个互不重叠的正方形？若能，求出是第几次画线后得到的；若不能，请说明理由．
答案解析收藏纠错 + 选题
22. (2020·定兴模拟) 一个不透明的口袋中有4个大小、质地完全相同的乒乓球，球面上都各标一个不小于－2的数，已知其中3个乒乓球上标的数分别是－2，2，4，所标的4个数的中位数是0．
1. （1）求这4个数的众数；
2. （2）从这个口袋中随机摸出1个球，求摸出的球面上的数是正数的概率；
3. （3）从这个口袋中随机摸出1个球（不放回），再从余下的球中随机摸出1个球，用列表法求两次摸出的球面上的数之和为负数的概率．
答案解析收藏纠错 + 选题
23. (2020·定兴模拟) 如图1和图2，矩形ABCD中，E是AD的中点，P是BC上一点，AF∥PD，∠FPE=∠DPE．
1. （1）作射线PE交直线AF于点G，如图1．
  ①求证：AG=DP；
  
  ②若点F在AD下方，AF=2，PF=7，求DP的长．
2. （2）若点F在AD上方，如图2，直接写出PD，AF，PF的等量关系．
答案解析收藏纠错 + 选题
24. (2020·定兴模拟) 甲、乙二人均从A地出发，甲以60米/分的速度向东匀速行进，10分钟后，乙以（60＋m）米/分的速度按同样的路线去追赶甲，乙出发5.5分钟后，甲以原速原路返回，在途中与乙相遇，相遇后两人均停止行进．设乙所用时间为t分钟．
1. （1）当m=6时，解答：
  ①设甲与A地的距离为 $\text{[math]}$ ，分别求甲向东行进及返回过程中， $\text{[math]}$ 与t的函数关系式（不写t的取值范围）；
  
  ②当甲、乙二人在途中相遇时，求甲行进的总时间．
2. （2）若乙在出发9分钟内与甲相遇，求m的最小值．
答案解析收藏纠错 + 选题
25. (2020·定兴模拟) 如图1，△ABC中，∠ACB=90°，AC=3，BC=4，延长BC到点D，使BD=BA，P是BC边上一点．点Q在射线BA上，PQ=BP，以点P为圆心，PD长为半径作⊙P，交AC于点E，连接PQ，设PC=x．
1. （1） AB=，CD=，当点Q在⊙P上时，x=；
2. （2） x为何值时，⊙P与AB相切？
3. （3）当PC=CD时，求阴影部分的面积；
4. （4）若⊙P与△ABC的三边有两个公共点，直接写出x的取值范围．
答案解析收藏纠错 + 选题
26. (2021九上·安义月考) 如图，函数y=－x²＋ $\text{[math]}$ x＋c（－2020≤x≤1）的图象记为L₁ ，最大值为M₁；函数y=－x²＋2cx＋1（1≤x≤2020）的图象记为L₂ ，最大值为M₂ ． L₁的右端点为A，L₂的左端点为B，L₁ ， L₂合起来的图形记为L．
1. （1）当c=1时，求M₁ ， M₂的值；
2. （2）若把横、纵坐标都是整数的点称为“美点”，当点A，B重合时，求L上“美点”的个数；
3. （3）若M₁ ， M₂的差为 $\text{[math]}$ ，直接写出c的值．
答案解析收藏纠错 + 选题