2019-2020学年初中数学八年级下学期期末模拟试卷（1）...

更新时间：2020-06-24 浏览次数：434 类型：期末考试

一、单选题

1. (2024八下·拱墅期末) 函数 $\text{[math]}$ 中自变量 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020八下·建湖月考) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021八下·庐江期末) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·银川期中) 用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（）

A . 有一个内角小于90° B . 每一个内角都大于90° C . 有一个内角小于或等于90° D . 每一个内角都小于90°

答案解析收藏纠错 + 选题
5. (2020·石家庄模拟) 如图，点 $\text{[math]}$ （ $\text{[math]}$ ）是反比例函数 $\text{[math]}$ 上的动点，过 $\text{[math]}$ 分别作 $\text{[math]}$ 轴， $\text{[math]}$ 轴的垂线，垂足分别为 $\text{[math]}$ ， $\text{[math]}$ .随着 $\text{[math]}$ 的增大，四边形 $\text{[math]}$ 的面积（）

A . 增大 B . 减小 C . 不确定 D . 不变

答案解析收藏纠错 + 选题
6. (2020·濉溪模拟) 为了更好地培养学生的合作意识，某校采用“团队合作学习”的模式进行学习，学期结束班主任对各小组合作学习的情况进行了综合评分．下表是其中一周的统计数据：

组别

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

分值

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

这组数据的众数和中位数分别是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020八下·安庆期中) 关于x的一元二次方程x²+（m﹣2）x+m+1=0有两个相等的实数根，则m的值是（）

A . 0 B . 8 C . 4±2 D . 0或8

答案解析收藏纠错 + 选题
8. (2023八下·香河期末) 如图，在四边形ABCD中，AC与BD相交于点O ，下列条件不能判定四边形ABCD为平行四边形的是（）

A . AB∥DC ， AB=DC B . AB=DC ， AD=BC C . AB∥DC ， AD=BC D . OA=OC ， OB=OD

答案解析收藏纠错 + 选题
9. (2021八下·海拉尔期末) 如图，由25个点构成的5×5的正方形点阵中，横、纵方向相邻的两点之间的距离都是1个单位.定义：由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A，B为顶点，面积为4的阵点平行四边形的个数为（）

A . 6个 B . 7个 C . 9个 D . 11个

答案解析收藏纠错 + 选题
10. (2020八上·海拉尔期末) 定义新运算： $\text{[math]}$ ，例如： $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2020·顺德模拟) 若一个多边形的内角和是外角和的3倍，则该多边形是边形（填该多边形的边数）．

答案解析收藏纠错 + 选题
12. (2020·杭州模拟) 在本学期的五次数学检测中，甲同学的成绩是： $\text{[math]}$ ，乙同学的成绩是： $\text{[math]}$ ，两名同学成绩比较稳定的是 (填“甲”或“乙”) .

答案解析收藏纠错 + 选题
13. (2020八上·萧山期中) 如图，△ABC的面积是16，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是．

答案解析收藏纠错 + 选题
14. (2019九上·杭州开学考) 如图，在正方形ABCD中，AB=6，E为CD上一动点，AE交BD于点F，过F作FH⊥AE，交BC于点H，连结AH、HE，AH与BD交于点G，下列结论：①AF=HE，②∠HAE=45°，③BG²+DF²=GF² ， ④△CEH的周长为12，其中正确的结论有。

答案解析收藏纠错 + 选题
15. (2024八下·广东期中) 菱形两邻角的比为 $\text{[math]}$ ，边长为2．则该菱形的面积为．

答案解析收藏纠错 + 选题
16. (2020·阜宁模拟) 如图，在平面直角坐标系中，反比例函数 $\text{[math]}$ 与正比例函数 $\text{[math]}$ 的图像分别交于点A、B，若∠AOB＝45°，则△AOB的面积是.

答案解析收藏纠错 + 选题

三、解答题

17. (2020八下·昌吉期中) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2020八下·哈尔滨期中) 解下列方程
1. （1）（3x－1）²＝2（3x－1）
2. （2） 3x²－2 $\text{[math]}$ x＋1＝0
答案解析收藏纠错 + 选题
19. (2020八下·德州期中) 如图，在菱形ABCD中，对角线AC、BD相交于点O，过A作 $\text{[math]}$ ，过D作 $\text{[math]}$ 与DE相交于点E.求证：四边形AODE为矩形.

答案解析收藏纠错 + 选题
20. (2019九上·江岸月考) 如图7，已知平行四边形ABCD的周长是32cm，AB︰BC=5︰3，AE⊥BC，垂足为E，AF⊥CD，垂足为F，∠EAF=2∠C.
1. （1）求∠C的度数；
2. （2）已知DF的长是关于 $\text{[math]}$ 的方程 $\text{[math]}$ - $\text{[math]}$ -6=0的一个根，求该方程的另一个根.
答案解析收藏纠错 + 选题

21. (2019八下·温岭期末) 王达和李力是八(2)班运动素质最好的两位同学，为了选出一名同学参加全校的体育运动大寒，班主任针对学校要测试的五个项目，对两位同学进行相应的测试(成绩：分)，结果如下：

姓名	力量	速度	耐力	柔韧	灵敏
王达	60	75	100	90	75
李力	70	90	80	80	80

根据以上测试结果解答下列问题：

（1）补充完成下表：

姓名	平均成绩(分)	中位数(分)	众数(分)	方差(分²)
王达	80	75	75	190
李力

（2）任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由；
（3）若按力量：速度：耐力：柔韧：灵敏=1：2：3：3：1的比例折合成综合分数，推选得分同学参加比赛，请通过计算说明应推选哪位同学去参赛。

答案解析收藏纠错 + 选题

22. (2020八下·安庆期中) 随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业．据统计，目前广东5G基站的数量约1.5万座，计划到2020年底，全省5G基站数量是目前的4倍，到2022年底，全省5G基站数量将达到17.34万座．
1. （1）计划到2020年底，全省5G基站的数量是多少万座？
2. （2）按照计划，求2020年底到2022年底，全省5G基站数量的年平均增长率；
3. （3）求2021年底全省5G基站的数量．
答案解析收藏纠错 + 选题
23. (2020九下·贵港模拟) 如图，已知直线y＝x﹣3与双曲线y＝ $\text{[math]}$ （k＞0）交于A、B两点，点A的纵坐标为1.
1. （1）求点B的坐标；
2. （2）直接写出当x在什么范围内时，代数式x²﹣3x的值小于k的值；
3. （3）点C（2，m）是直线AB上一点，点D（n，4）是双曲线y＝ $\text{[math]}$ 上一点，将△OCD沿射线BA方向平移，得到△O′C′D′.若点O的对应点O′落在双曲线y＝ $\text{[math]}$ 上，求点D的对应点D′的坐标.
答案解析收藏纠错 + 选题
24. (2020·南岸模拟) 如图1和图2，在△ABC中，AB＝13，BC＝14， $\text{[math]}$ .
1. （1）探究：
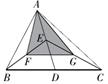
  如图1，AH⊥BC于点H，则AH＝，AC＝，△ABC的面积 $\text{[math]}$ ＝.
2. （2）拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD＝x，AE＝m，CF＝n，（当点D与A重合时，我们认为 $\text{[math]}$ ＝0）.
  用含x、m或n的代数式表示 $\text{[math]}$ 及 $\text{[math]}$ ；
3. （3）求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；
4. （4）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围.
  发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2019-2020学年初中数学八年级下学期期末模拟试卷（1）...

副标题：

*注意事项：

2019-2020学年初中数学八年级下学期期末模拟试卷（1）...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

组别	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
分值	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$