一、选择题(本题有10小题,每小题3分,共30分)
-
-
A . 5
B . 2
C . -2
D . -5
-
-
-
5.
(2021·酒泉模拟)
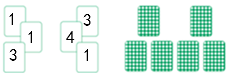
如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )
-
A . 连结直线外一点与直线上各点的所有线段中,垂线段最短
B . 在同一平面内,垂直于同一条直线的两条直线互相平行
C . 在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线
D . 经过直线外一点,有且只有一条直线与这条直线平行
-
7.
已知点(-2,a),(2,b),(3,c)在函数

的图象上,则下列判断正确的是( )
A . a<b<c
B . b<a<c
C . a<c<b
D . c<b<a
-
8.
(2020九上·奎文期末)
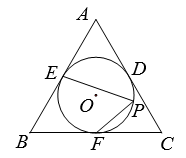
如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是

上一点,则∠EPF的度数是( )
A . 65°
B . 60°
C . 58°
D . 50°
-
9.
(2022七上·句容期末)
如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是( )

-
10.
(2020·金华·丽水)
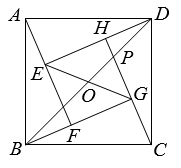
如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH . 连结EG,BD相交于点O,BD与HC相交于点P.若GO=GP,则

的值是( )
二、填空题 (本题有6小题,每小题4分,共24分)
-
-
-
-
14.
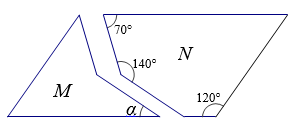
如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是
°.
-
15.
(2020·金华·丽水)
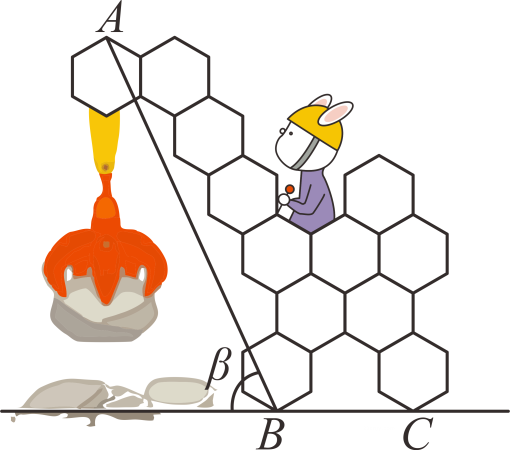
如图是小明画的卡通图形,每个正六边形的边长都相等,相邻两正六边形的边重合,点A,B,C均为正六边形的顶点,AB与地面BC所成的锐角为β,则tanβ的值是
.
-
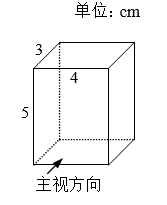
16.
(2020·金华·丽水)
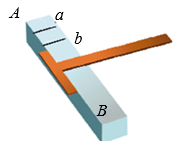
图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm, CE=DF, CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.

-
(1)
当E,F两点的距离最大值时,以点A,B,C,D为顶点的四边形的周长是cm.
-
(2)
当夹子的开口最大(点C与点D重合)时,A,B两点的距离为cm.
三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程)
-
-
-
19.
(2020·金华·丽水)
某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
抽取的学生最喜爱体育锻炼项目的统计表
| 类别 |
项目 |
人数(人) |
| A |
跳舞 |
59 |
| B |
健身操 |
|
| C |
俯卧撑 |
31 |
| D |
开合跳 |
|
| E |
其它 |
22 |

-
-
(2)
在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
-
(3)
该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
-
-
-
(2)
求
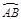
的长.
-
21.
(2020·金华·丽水)
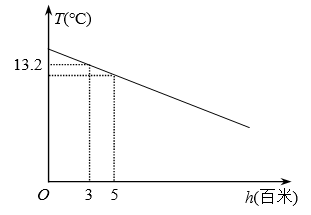
某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
-
-
-
-
-
-
(2)
点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
-
23.
(2020·金华·丽水)
如图,在平面直角坐标系中,已知二次函数
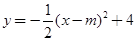
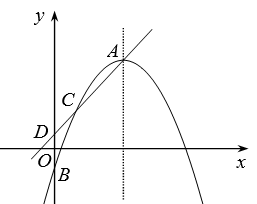
图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
-
-
(2)
当n=2时,若点A在第一象限内,结合图象,求当y
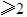
时,自变量x的取值范围.
-
(3)
作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.
-
24.
(2020·金华·丽水)
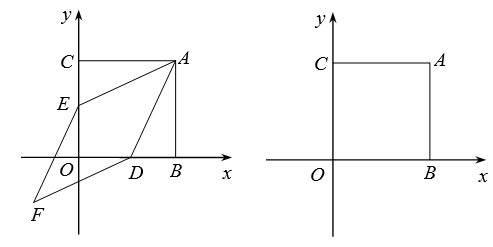
如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F, 已知OB=8.
-
-
-
(3)
若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.
 B .
B .  C .
C .  D .
D .