湖南省醴陵市2018-2019学年七年级下学期数学期末试卷

更新时间：2024-07-13 浏览次数：272 类型：期末考试

一、单选题

1. (2019七下·醴陵期末) 下列图形中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020·沭阳模拟) 下列计算正确的是（　　）

A . x²+x²=x⁴ B . (x﹣y)²=x²﹣y² C . (﹣x)²•x³=x⁵ D . (x²y)³=x⁶y

答案解析收藏纠错 + 选题
3. (2019七下·醴陵期末) 下列说法正确的是（）

A . 同旁内角相等，两直线平行 B . 两直线平行，同位角互补 C . 相等的角是对顶角 D . 等角的余角相等

答案解析收藏纠错 + 选题
4. (2019七下·醴陵期末) 2019年我国部分省份发生了猪瘟疫情，经科学家检测猪瘟病毒的直径是0.000000042米，将0.000000042用科学记数法表示为（）

A . 4.2×10^－⁹ B . 4.2×10^－⁸ C . 0.42×10^－⁸ D . 42×10^－⁹

答案解析收藏纠错 + 选题

5. (2019七下·醴陵期末) 下表是某公司员工月收入的资料：

月收入/元	45000	18000	10000	5500	5000	3400	3300	1000
人数	1	1	1	3	6	1	11	1

能够反映该公司全体员工月收入水平的统计量是（）

A . 平均数和众数 B . 平均数和中位数 C . 中位数和众数 D . 平均数和方差

答案解析收藏纠错 + 选题

6. (2019七下·醴陵期末) 分式 $\text{[math]}$ 的计算结果是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020八上·郓城期末) 如图，下列说法错误的是(　　)

A . 因为∠BAD＋∠ADC＝180°，所以AB∥CD B . 因为AB∥CD，所以∠BAC＝∠ACD C . 因为∠ABD＝∠CDB，所以AD∥BC D . 因为AD∥BC，所以∠BCA＝∠DAC

答案解析收藏纠错 + 选题
8. (2023八上·吴忠期末) 图（1）是一个长为2m，宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（）

A . 2mn B . （m+n）² C . （m-n）² D . m²-n²

答案解析收藏纠错 + 选题
9. (2020八上·福清期末) 如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC=62°，则∠DFE的度数为（）

A . 31° B . 28° C . 62° D . 56°

答案解析收藏纠错 + 选题
10. (2021七下·卢龙期中) 已知a²+a﹣4=0，那么代数式：a²（a+5）的值是（ )

A . 4 B . 8 C . 12 D . 16

答案解析收藏纠错 + 选题

二、填空题

11. (2020八下·永春期末) 若分式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
12. (2019七下·醴陵期末) $\text{[math]}$ =。

答案解析收藏纠错 + 选题
13. (2019七下·醴陵期末) 如果一组数据6、7、x、10、5的众数是7，那么这组数据的平均数为。

答案解析收藏纠错 + 选题
14. (2019七下·醴陵期末) $\text{[math]}$ =。

答案解析收藏纠错 + 选题
15. (2024七上·奉贤月考) 若a^m=2，aⁿ=3，则a^m+2n=.

答案解析收藏纠错 + 选题
16. (2019七下·醴陵期末) 若m- $\text{[math]}$ =3，则m²+ $\text{[math]}$ =．

答案解析收藏纠错 + 选题
17. (2019七下·醴陵期末) 如图，已知△ABC的面积为16，BC的长为8，现将△ABC沿BC向右平移m个单位到△A′B′C′的位置。若四边形ABB′A′的面积为32，求m=。

答案解析收藏纠错 + 选题
18. (2019七下·醴陵期末) 如图所示，直线a∥b，∠1=35°，∠2=90°，则∠3的度数为。

答案解析收藏纠错 + 选题

三、解答题

19. (2019七下·醴陵期末) 因式分解：
①a²(x﹣y)+4b²(y﹣x)

答案解析收藏纠错 + 选题
20. (2019七下·醴陵期末) 先化简，再求值: $\text{[math]}$ ,其中x=-1.

答案解析收藏纠错 + 选题
21. (2019七下·醴陵期末) 先化简： $\text{[math]}$ ，然后在－2，2，3，0中选一个合适的数代入求值。

答案解析收藏纠错 + 选题

22. (2019七下·醴陵期末) 为了参加“醴陵市中小学生首届诗词大会”,某中学八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77 ,92, 85;八(2)班79 ,85 ,92,85 ,89.通过数据分析,列表如下:

班级	平均分	中位数	众数	方差
八(1)	85	b	c	d
八(2)	a	85	85	e

（1）直接写出表中a,b,c的值：a=,b= ,c=.
（2）求d,e的值，并根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
（3）若“醴陵市中小学生首届诗词大会”中，各中学代表队成绩计分分两部分：现场评委记分和网络评委投票记分。且现场评委记分权数为80%，网络评委投票记分权数为20%，请计算A,B,C三所中学代表队的最终得分为多少？

中学A

中学B

中学C

评委记分

90

80

85

网络投票记分

85

92

88

答案解析收藏纠错 + 选题

23. (2019七下·醴陵期末) 如图，△ABC的顶点A，B，C均在正方形网格的格点上．
1. （1）画出△ABC关于直线m的对称图形△A₁B₁C₁；
2. （2）画出将△ABC向下平移5个单位，再沿水平方向向左平移6个单位后，最后得到的A₂B₂C₂；
3. （3）画出将△ABC绕点A顺时针旋转90°后，所得到的图形，△AB₃C₃；
答案解析收藏纠错 + 选题
24. (2019七下·醴陵期末) 填空并完成以下证明：
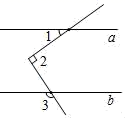
已知：点P在直线CD上，∠BAP+∠APD=180°，∠1=∠2．

求证：AB∥CD，∠E=∠F．

证明：∵∠BAP+∠APD=180°，（已知）

∴AB∥．（）

∴∠BAP=．（）

又∵∠1=∠2，（已知）

∠3=﹣∠1，

∠4=﹣∠2，

∴∠3=（等式的性质）

∴AE∥PF．（）

∴∠E=∠F．（）

答案解析收藏纠错 + 选题
25. (2019七下·醴陵期末) 阅读材料：我们知道：若几个非负数相加得零，则这些数都必同时为零。
例如：①（a﹣1）²+（b+5）²=0，我们可以得：（a﹣1）²=0，（b+5）²=0，∴a=1，b=-5．

②若m²-4m+n²+6n+13=0，求m、n的值．

解：∵m²-4m+n²+6n+13=0，

∴（m²﹣4m+4)+(n²+6n+9)=0(我们将13拆成4和9，等式左边就出现了两个完全平方式）

∴(m﹣2)²+(n+3)²=0，

∴(m﹣2)²=0，(n+3)²=0，

∴ n=2，m=-3．

根据你的观察，探究下面的问题：
1. （1） a²﹣4a+4+b²=0，则a=．b=．
2. （2）已知x²+2xy+2y²－6y+9=0，求x^y的值．
3. （3）已知a、b（a≠b）是等腰三角形的边长，且满足2a²+b²﹣8a﹣6b+17=0，求三角形的周长。
答案解析收藏纠错 + 选题
26. (2019七下·醴陵期末) 已知：∠A=（90+x）°，∠B=（90﹣x）°，∠CED=90°，射线EF∥AC，2∠C﹣∠D=m.
1. （1）判断AC与BD的位置关系，并说明理由．
2. （2）如图1，当m=30°时，求∠C、∠D的度数．
3. （3）如图2，求∠C、∠D的度数（用含m的代数式表示）．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

湖南省醴陵市2018-2019学年七年级下学期数学期末试卷

副标题：

*注意事项：

湖南省醴陵市2018-2019学年七年级下学期数学期末试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

	中学A	中学B	中学C
评委记分	90	80	85
网络投票记分	85	92	88