 B .
B .  C .
C .  D .
D . 




1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
|
分数 人数 班级 |
60 |
70 |
80 |
90 |
100 |
|
1班 |
0 |
1 |
6 |
2 |
1 |
|
2班 |
1 |
1 |
3 |
a |
1 |
|
3班 |
1 |
1 |
4 |
2 |
2 |
分析数据:
|
平均数 |
中位数 |
众数 |
|
|
1班 |
83 |
80 |
80 |
|
2班 |
83 |
c |
d |
|
3班 |
b |
80 |
80 |
根据以上信息回答下列问题:
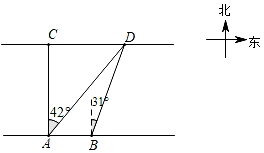
①当∠FCD的度数为时,四边形OADC是菱形;
②若AB=2 ,当CF∥AB时,DF的长为.
|
品牌 |
A |
B |
|
进价(元/台) |
120 |
180 |
|
售价(元/台) |
150 |
240 |
|
x |
… |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
3 |
m |
1 |
0 |
1 |
2 |
1 |
n |
|
… |
其中,m= , n=.
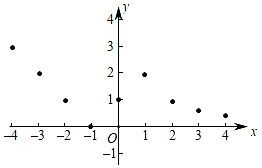
①点A( ,y1),B(5,y2),C(x1 ,
),D(x2 , 6)在函数图象上,则y1 ▲ y2 , x1 ▲ x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
如图1,△ABC和△ADE均为等边三角形,点D在BC边上,连接CE.

填空:
①∠DCE的度数是;
②线段CA、CE、CD之间的数量关系是.
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在BC边上,连接CE.请判断∠DCE的度数及线段CA、CE、CD之间的数量关系,并说明理由.
如图3,在Rt△ABC中,∠A=90°,AC=4,AB=6.若点D满足DB=DC,且∠BDC=90°,请直接写出DA的长.
