
 B .
B .  C .
C .  D .
D . 
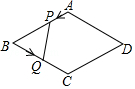
 B .
B . 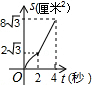 C .
C .  D .
D . 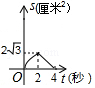
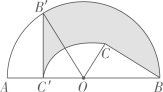
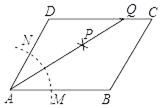


根据图中信息解决下列问题:


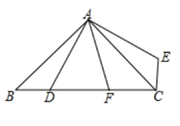
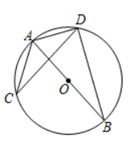
①如图,当点F在线段BC上,猜想线段BD,DF,FC之间的数量关系,并证明;
②若BD=6,CF=8,直接写出AD的长.
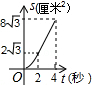
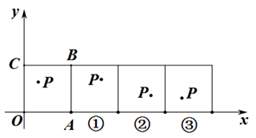
①求点 的坐标和
的面积;
②在直线 上是否存在点
,使
为直角三角形?若存在,直接写出符合条件的所有点
的坐标;若不存在,请说明理由.