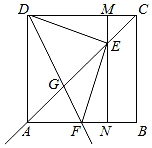
B .
B .  C .
C .  D .
D . 金额 | 50 | 100 | 200 | 500 | 1000 |
人数 | 6 | 17 | 14 | 8 | 5 |
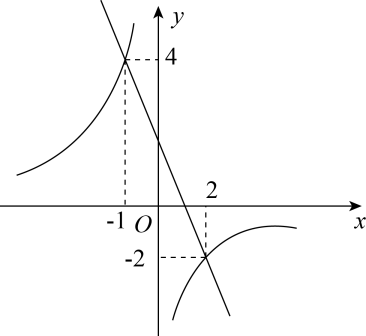
 B .
B .  C .
C .  D .
D . 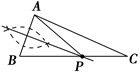
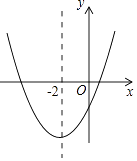

|
类别 |
频数(人数) |
频率 |
|
小说 |
0.5 |
|
|
戏剧 |
4 |
|
|
散文 |
10 |
0.25 |
|
其他 |
6 |
|
|
合计 |
m |
1 |

请根据以上信息,解答下列问题: