浙江省绍兴市诸暨市2020届九年级适数学适应性试卷

更新时间：2020-09-24 浏览次数：514 类型：中考模拟

一、选择题(本大题有10小题，每小题4分，共40分.请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分)

1. (2020·诸暨模拟) 5的相反数是（）

A . -5 B . 5 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·诸暨模拟) 众志成城，抗击疫情。今年春节新冠肺炎在武汉大肆流行，社会各界纷纷支援武汉。截止1月31日，武汉共收到社会捐款2 586 000 000元，数字2 586 000 000用科学记数法可以表示为（）

A . 25.86×10⁸ B . 2.586×10⁹ C . 2.586×10⁸ D . 0.2586×10¹⁰

答案解析收藏纠错 + 选题
3. (2020·诸暨模拟) 由6个相同的立方体搭成的几何体如图所示，则它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·诸暨模拟) 下列运算正确的是（）

A . (ab³)²=a²b⁶ B . 2a+3b=5ab C . 5a²-3a²=2 D . (a+1)²=a²+1

答案解析收藏纠错 + 选题

5. (2020·诸暨模拟) 一次数学测试，某小组5名同学的成绩统计如下(有两个数据被遮盖)：

组员	甲	乙	丙	丁	戊	平均成绩	众数
得分	81	77	■	80	82	80	●

则被遮盖的两个数据依次是（）

A . 80，80 B . 81，80 C . 80，2 D . 81，2

答案解析收藏纠错 + 选题

6. (2020·诸暨模拟) 如图，以点O为位似中心，把△ABC放大为原图形的2倍得到△A'B'C'，以下说法中错误的是（）

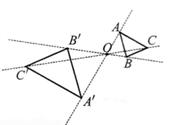
A . △ABC∽△A'B'C' B . 点C、点O、点C'三点在同一直线上 C . AO：AA'=1∶2 D . AB∥A'B'

答案解析收藏纠错 + 选题
7. (2020·诸暨模拟) 某中学有一块长30m，宽20m的矩形空地，计划在这块空地上划出四分之一的区域(阴影部分)种花，某同学设计方案如图所示，求花带的宽度.设花带的宽度为x(m)，则可列方程是（）

A . (30-x)(20-x)= $\text{[math]}$ ×20×30 B . (30-2x)(20-x)= $\text{[math]}$ ×20×30 C . 30x+2×20x== $\text{[math]}$ ×20×30 D . (30-2x)(20-x)= $\text{[math]}$ ×20×30

答案解析收藏纠错 + 选题
8. (2020·诸暨模拟) 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容

已知：如图，∠BEC=∠B+∠C

求证：AB∥CD

证明：延长BE交★于点F，

则∠BEC=■+∠C(三角形的外角等于它不相等的内角之和)

又∠BEC=∠B+∠C，得∠B=▲

故AB∥CD(●相等，两直线平行).

则回答错误的是（）

A . ★代表CD B . ■代表∠EFC C . ▲代表∠EFC D . ●代表同位角

答案解析收藏纠错 + 选题
9. (2020·诸暨模拟) 如图，四边形ABCD是菱形，⊙O经过点A，C，D，与BC相交于点E，连接AC，AE。若∠D=80°，则∠EAC的度数是（）

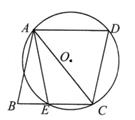
A . 20° B . 25° C . 30° D . 35°

答案解析收藏纠错 + 选题
10. (2020·诸暨模拟) 如图，在平面直角坐标系中，抛物线y=-(x-3m-1)(x+1)与y轴相交于点A，其中m>0，点B(0，1)，点M(a，1+b)在抛物线对称轴上，点N在坐标平面内。若以点A，B，M，N为顶点的四边形是菱形，则 $\text{[math]}$ 的值不可能是（）

A . 1 B . 2+ $\text{[math]}$ C . $\text{[math]}$ D . 2- $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本大题有6小题，每小题5分，共30分.)

11. (2020·诸暨模拟) 分解因式：4x²-y²=。

答案解析收藏纠错 + 选题
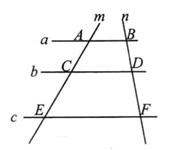
12. (2020·诸暨模拟) 如图，已知直线a∥b∥c，直线m，n与a，b，c分别交于点A，C，E和点B，D，F，若AC=3，CE=6，BD=2，则DF的值是。

答案解析收藏纠错 + 选题
13. (2020·诸暨模拟) 我国古代数学著作《九章算术》中记载：“今有大器五小器一容三斛，大器一小器五容二斛。问大小器各容几何.”其大意为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛(斛：古代的一种容量单位)。1个大桶加上5个小桶可以盛酒2斛，问1个大桶、一个小桶分别可以盛酒多少斛？若设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，根据题意，可列方程组得：。

答案解析收藏纠错 + 选题
14. (2020·诸暨模拟) 如图，在矩形ABCD中，对角线AC，BD交于点O，E是直线BC上一点，且BE=BO，连结AE。若∠BAC=60°，则∠CAE的度数是。

答案解析收藏纠错 + 选题
15. (2020·诸暨模拟) 如图，反比例函数y= $\text{[math]}$ (x>0)的图形经过A(2，6)和B两点，且tan∠AOB= $\text{[math]}$ ，则点B的坐标是。

答案解析收藏纠错 + 选题
16. (2020·诸暨模拟) 如图，直线l₁∥l₂∥l₃ ， A，B，C分别为直线l₁ ， l₂ ， l₃上的动点，连接AB，BC，AC，线段AC交直线l₂于点D。设直线l₁ ， l₂之间的距离为m，直线l₂ ， l₃之间的距离为n，若∠ABC=60°，BD=2 $\text{[math]}$ ，且 $\text{[math]}$ ，则m+n的最大值是。

答案解析收藏纠错 + 选题

三、解答题(本大题有8小题，第17~20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分.解答需写出必要的文字说明、演算步骤或证明过程)

17. (2020·诸暨模拟)
1. （1）计算：|-3|+2^-1-( $\text{[math]}$ )⁰ -sin30°
2. （2）解方程：x²-2x-3=0
答案解析收藏纠错 + 选题
18. (2020·诸暨模拟) 某校在课改中，开设的选修课有：篮球，足球，排球，羽毛球，乒乓球，学生可根据自己的爱好选修一门，李老师对九(1)班全班同学的选课情况进行调查统计，制成了两幅不完整的统计图(如图)。
1. （1）该班共有学生人，并补全条形统计图。
2. （2）求“篮球”所在扇形圆心角的度数。
3. （3）九(1)班班委4人中，甲选修篮球，乙和丙选修足球，丁选修排球，从这4人中任选2人，请你用列表或画树状图的方法，求选出的2人中恰好为1人选修篮球，1人选修足球的概率。
答案解析收藏纠错 + 选题
19. 如图，在 $\text{[math]}$ 的网格中，每个小正方形的边长为1，点A在格点（小正方形的顶点）上．试在各网格中画出顶点在格点上，面积为6，且符合相应条件的图形．

答案解析收藏纠错 + 选题
20. (2020·诸暨模拟) 如图，正方形ABCD的边长为4cm，动点P从A点出发，在正方形的边上由A→B→C→D运动，设运动的时间为t(s)，△APD的面积为S(cm²)，S与t的函数图象如图所示。
1. （1）当点P在BC上运动时，写出t的范围。
2. （2）当t为何值时，△APD的面积为6cm²。
答案解析收藏纠错 + 选题
21. (2021九上·宁波期中) 如图，某学校体育场看台的顶端C到地面的垂直距离CD为2m，看台所在斜坡CM的坡比i=1：3，在点C处测得旗杆顶点A的仰角为30°，在点M处测得旗杆顶点A的仰角为60°，且B，M，D三点在同一水平线上。
1. （1）求DM的长。
2. （2）求旗杆AB的高度。(结果保留根号)
答案解析收藏纠错 + 选题
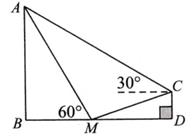
22. (2020·诸暨模拟) 在平面直角坐标系中，一次函数y=kx+6(k≠0)的图象分别与x轴，y轴相交于点A，点B。点P在线段AB上，过点P分别作x轴，y轴的垂线段PC，PD，垂足为C，D。
1. （1）若k=-1，如图。
  ①求矩形OCPD的周长。
  
  ②求矩形OCPD面积的最大值。
2. （2）若矩形OCPD的面积最大值为6，求k的值。
答案解析收藏纠错 + 选题
23. (2020·诸暨模拟) 如果三角形有一边上的中线恰好等于这条边长，那么称这个三角形为“和谐三角形”。
1. （1）如图1，在6×6的网格中，每个小正方形的边长为1，点A，B都在格点(小正方形的顶点)上，在网格中找一个格点C，使得△ABC为“和谐三角形”。
2. （2）如图2，△ABC中，∠ACB=90°，AB=2 $\text{[math]}$ ，BC=2 $\text{[math]}$ 。求证：△ABC是“和谐三角形”。
3. （3）如图3，点M，N在抛物线y=x²上，且MN∥x轴，若△OMN是“和谐三角形”，求点N的坐标。
答案解析收藏纠错 + 选题
24. (2020·诸暨模拟) 已知：在Rt△ABC中，∠ABC=90°，点D为边BC上一动点，以BD为直径作圆，记其圆心为O，连结AD交⊙O于点E，过点B作BF∥AC，交⊙O于点F。设 $\text{[math]}$ =k。
1. （1）如图1，连结EF，BE。若k= $\text{[math]}$ ，AB=6。
  ①当∠BFE=45°时，求BD的长。
  
  ②当△BFE为等腰三角形时，求所有满足条件的BD的长。
2. （2）点D与点C重合，如图2。连结AF与⊙O的另一交点为M，若点M是线段AF的中点，请直接写出k²的值。
答案解析收藏纠错 + 选题