 B .
B .  C .
C .  D .
D . 
如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

 B .
B . 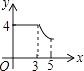 C .
C .  D .
D . 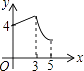
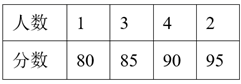



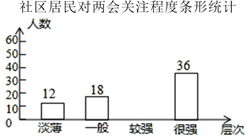
请结合图表中的信息,解答下列问题:
(参考数据: )

(ⅰ)若想每天获利18000元,该公司应该把销售单价定为多少元?
(ⅱ)该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?
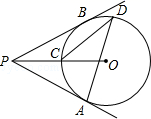
①连接BC,若△BOC与△AMN相似,请直接写出t的值;
②△AOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.