北京市西城区北京教育学院附属中学2019-2020学年九年级...

更新时间：2024-07-13 浏览次数：473 类型：期中考试

一、单选题

1. (2019九上·西城期中) 下列图形中，既是轴对称图形又是中心对称图形的是 $\text{[math]}$ 　　 $\text{[math]}$

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·义乌期末) 二次函数y=（x﹣5）²+7的最小值是（）

A . ﹣7 B . 7 C . ﹣5 D . 5

答案解析收藏纠错 + 选题
3. (2019九上·西城期中) 如图，AB、CD是⊙O的两条弦，连结AD、BC ．若∠BCD＝70°，则∠BAD的度数为（　　）

A . 40° B . 50° C . 60° D . 70°

答案解析收藏纠错 + 选题
4. (2019九上·西城期中) 如图，在⊙O中，CD是直径，AB是弦，于M，，，则MD的长为（）

A . 4 B . 2 C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
5. (2019九上·西城期中) 下列说法正确的是（）

A . 长度相等的两条弧是等弧 B . 平分弦的直径垂直于弦 C . 直径是同一个圆中最长的弦 D . 过三点能确定一个圆

答案解析收藏纠错 + 选题
6. (2021九上·赣州期中) 把抛物线y=x²+1向右平移3个单位，再向下平移2个单位，得到抛物线（）

A . y=（x+3）²﹣1 B . y=（x+3）²+3 C . y=（x﹣3）²﹣1 D . y=（x﹣3）²+3

答案解析收藏纠错 + 选题
7. (2019九上·西城期中) 已知二次函数y=ax²+bx+c的图象如图所示，则a、b、c满足（）

A . a＜0，b＜0，c＞0 B . a＜0，b＜0，c＜0 C . a＜0，b＞0，c＞0 D . a＞0，b＜0，c＞0

答案解析收藏纠错 + 选题
8. (2019九上·西城期中) 如图，圆弧形拱桥的跨径 $\text{[math]}$ 米，拱高 $\text{[math]}$ 米，则拱桥的半径为（）米

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·攀枝花模拟) 二次函数 $\text{[math]}$ 的部分图象如图所示，则下列结论中正确的是（）．

A . $\text{[math]}$ B . 不等式 $\text{[math]}$ 的解集是 $\text{[math]}$ C . $\text{[math]}$ D . 当 $\text{[math]}$ 时，y随x的增大而增大

答案解析收藏纠错 + 选题
10. (2019九上·西城期中) 如图，△ABC中，∠B=60，∠ACB=75，点D是BC边上一动点，以AD为直径作⊙O ，分别交AB、AC于E、F ，若弦EF的最小值为1，则AB的长为

A . B . C . 1.5 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、解答题

11. (2019九上·西城期中) △ABC在平面直角坐标系中的位置如图所示，其中A（1，2），B（1，1），C（3，1），将△ABC绕原点O顺时针旋转90°后得到△A′B′C′，画出△A′B′C′，并求点A旋转到点A′所经过的路线长为．

答案解析收藏纠错 + 选题
12. (2024九上·珠海月考) 已知抛物线的顶点为(-1，-3)，与y轴的交点为(0，-5)求抛物线的解析式.

答案解析收藏纠错 + 选题
13. (2019九上·西城期中) 如图，PA、PB是⊙O的切线，A、B为切点，∠OAB＝30°．
1. （1）求∠APB的度数；
2. （2）当OA＝3时，求AP的长．
答案解析收藏纠错 + 选题
14. (2019九上·西城期中) 一件轮廓为圆形的文物出土后只留下了一块残片，文物学家希望能把此件文物进行复原，如图所示，请你帮助文物学家作出此文物轮廓圆心O的位置（要求：尺规作图，保留作图痕迹，不写作法）．

答案解析收藏纠错 + 选题
15. (2019九上·西城期中) 如图，四边形ABCD中，∠BAD＝∠C＝90°，AB＝AD ， AE⊥BC于E ，若线段AE＝5，BE＝2，则S_四边形_ABCD的面积为多少？

答案解析收藏纠错 + 选题
16. (2019九上·西城期中) 已知二次函数的解析式是y＝x²﹣2x﹣3．
1. （1）与y轴的交点坐标是，顶点坐标是．
2. （2）在坐标系中利用描点法画出此抛物线；
  
  x
  
  …
  
  …
  
  y
  
  …
  
  …
3. （3）结合图象回答：当﹣2＜x＜2时，函数值y的取值范围是．
答案解析收藏纠错 + 选题
17. (2019九上·西城期中) 已知：如图，AB是⊙O的直径，BC是弦，∠B＝30°，延长BA到D，使∠BDC＝30°．
1. （1）求证：DC是⊙O的切线；
2. （2）若AB＝2，求DC的长．
答案解析收藏纠错 + 选题
18. (2021九上·凤山期中) 已知抛物线y=x²﹣（2m﹣1）x+m²﹣m．
1. （1）求证：此抛物线与x轴必有两个不同的交点；
2. （2）若此抛物线与直线y=x﹣3m+3的一个交点在y轴上，求m的值．
答案解析收藏纠错 + 选题
19. (2020九上·定南期中) 某工厂设计了一款产品，成本为每件20元．投放市场进行试销，经调查发现，该种产品每天的销售量y（件）与销售单价x（元）之间满足y=﹣2x+80(20≤x≤40)，设销售这种产品每天的利润为W（元）．
1. （1）求销售这种产品每天的利润W（元）与销售单价x（元）之间的函数表达式；
2. （2）当销售单价定为多少元时，每天的利润最大？最大利润是多少元？
答案解析收藏纠错 + 选题

20. (2019九上·西城期中) 有这样一个问题：探究函数y= $\text{[math]}$ x²+ $\text{[math]}$ 的图象与性质.

小东根据学习函数的经验，对函数y= $\text{[math]}$ x²+ $\text{[math]}$ 的图象与性质进行了探究.

下面是小东的探究过程，请补充完整：

（1）函数y= $\text{[math]}$ x²+ $\text{[math]}$ 的自变量x的取值范围是；

（2）下表是y与x的几组对应值.

…

﹣3

﹣2

﹣1

﹣ $\text{[math]}$

$\text{[math]}$

…

$\text{[math]}$

﹣ $\text{[math]}$

$\text{[math]}$

…

标格中m的值为m=；

（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1， $\text{[math]}$ ），结合函数的图象，写出该函数的其它性质（一条即可）.

答案解析收藏纠错 + 选题

21. (2019九上·西城期中) 以坐标原点为圆心，1为半径的圆分别交x，y轴的正半轴于点A，B．
1. （1）如图一，动点P从点A处出发，沿x轴向右匀速运动，与此同时，动点Q从点B处出发，沿圆周按顺时针方向匀速运动．若点Q的运动速度比点P的运动速度慢，经过1秒后点P运动到点（2，0），此时PQ恰好是⊙O的切线，连接OQ．求∠QOP的大小；
2. （2）若点Q按照（1）中的方向和速度继续运动，点P停留在点（2，0）处不动，求点Q再经过5秒后直线PQ被⊙O截得的弦长．
答案解析收藏纠错 + 选题
22. (2019九上·西城期中) 对于二次函数y＝x²﹣3x+2和一次函数y＝﹣2x+4，把y＝t（x²﹣3x+2）+（1﹣t）（﹣2x+4）称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线L ．现有点A（2，0）和抛物线L上的点B（﹣1，n），请完成下列任务：
1. （1）（尝试）
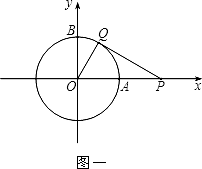
  当t＝2时，抛物线y＝t（x²﹣3x+2）+（1﹣t）（﹣2x+4）的顶点坐标为；
2. （2）判断点A是否在抛物线L上；
3. （3）求n的值；
4. （4）（发现）
  通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线L总过定点，坐标为．
5. （5）（应用）
  二次函数y＝﹣3x²+5x+2是二次函数y＝x²﹣3x+2和一次函数y＝﹣2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由．
答案解析收藏纠错 + 选题

三、填空题

23. (2019九上·西城期中) 点P（﹣2，y₁）和点Q（﹣1，y₂）分别为抛物线y＝x²﹣4x+3上的两点，则y₁y₂ ．（用“＞”或“＜”填空）．

答案解析收藏纠错 + 选题
24. (2022九上·上思期中) 由8时15分到8时40分，时钟的分针旋转的角度为．

答案解析收藏纠错 + 选题
25. (2022九上·嘉兴期中)
如图，将△ABC绕点A顺时针旋转60°得到△AED ，若线段AB=3，则BE=．

答案解析收藏纠错 + 选题
26. (2019九上·西城期中) 如图，AB、AC是⊙O的两条弦，∠A=30°，过点C的切线与OB的延长线交于点D ，则∠D=°．

答案解析收藏纠错 + 选题
27. (2020九上·北京期中) 二次函数y=ax²+bx的图象如图，若一元二次方程ax²+bx+m=0有实数根，则m的最大值为．

答案解析收藏纠错 + 选题
28. (2019九上·西城期中) 已知二次函数y＝ax²+bx+c中，其函数值y与自变量x之间的部分对应值如表所示：

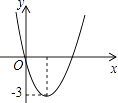
x

…

0

1

2

3

4

…

y

…

4

1

0

1

4

…

点A（x₁ ， y₁）、B（x₂ ， y₂）在函数的图象上，则当1＜x₁＜2，3＜x₂＜4时，y₁与y₂的大小关系是．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

北京市西城区北京教育学院附属中学2019-2020学年九年级...

副标题：

*注意事项：

北京市西城区北京教育学院附属中学2019-2020学年九年级...

试题分析

总体分析

题量分析

难度分析

知识点分析