北京市西城区宣武外国语实验学校2019-2020学年九年级上...

更新时间：2024-07-31 浏览次数：220 类型：期中考试

一、单选题

1. (2024九上·朝阳期中) 抛物线y＝x²+1的对称轴是（）

A . 直线x＝﹣1 B . 直线x＝1 C . 直线x＝0 D . 直线y＝1

答案解析收藏纠错 + 选题
2. (2020九上·泰兴期中) 如图，在△ABC中，DE∥BC，DE分别与AB，AC相交于点D，E，若AD=4，DB=2，则DE：BC的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019九上·西城期中) 如图是几种常见的汽车轮毂图案，图案围绕中心旋转90°后能与原来的图案重合的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019九上·西城期中) 如图所示，△ABC中∠BAC＝80°，AB＝4，AC＝6．甲、乙、丙、丁四名同学分别在△ABC内画出一个阴影三角形与△ABC相似，其中画的错误的是(　　)

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024九上·朝阳期中) 将抛物线 $\text{[math]}$ 向上平移 $\text{[math]}$ 个单位后得到的抛物线恰好与 $\text{[math]}$ 轴有一个交点，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·临清期中) 如图，每个小正方形的边长均为1，则下列图形中的三角形（阴影部分）与 $\text{[math]}$ 相似的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2021九上·福绵期中) 如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则 $\text{[math]}$ 的大小为（）

A . 30° B . 40° C . 50° D . 60°

答案解析收藏纠错 + 选题
8. (2023九上·萧山期中) 已知一个二次函数图象经过P₁（﹣3，y₁），P₂（﹣1，y₂），P₃（1，y₃），P₄（3，y₄）四点，若y₃＜y₂＜y₄ ，则y₁ ， y₂ ， y₃ ， y₄的最值情况是（　　）

A . y₃最小，y₁最大 B . y₃最小，y₄最大 C . y₁最小，y₄最大 D . 无法确定

答案解析收藏纠错 + 选题

二、填空题

9. (2021九上·榆林期中) 利用复印机的缩放功能，将原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形，则放大前后的两个三角形的面积比为．

答案解析收藏纠错 + 选题
10. (2019九上·西城期中) 老师给出一个二次函数，甲、乙、丙三名同学各指出这个函数的一个性质．
甲：函数图象的顶点在x轴上；

乙：当x＜1时，y随x的增大而减小；

丙：该函数的形状与函数y＝x²的图象相同

已知这三位同学的描述都正确，请你写出满足上述所有性质的一个二次函数表达式．

答案解析收藏纠错 + 选题
11. (2022九上·聊城期末)
如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD是米．

答案解析收藏纠错 + 选题
12. (2019九上·西城期中) 如图，在平面直角坐标系xOy中，△AOB可以看作是△OCD经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一中由△OCD得到△AOB的过程：．

答案解析收藏纠错 + 选题
13. (2019九上·西城期中) 如图，在平面直角坐标系xOy中，抛物线y＝ax²+bx+c与x轴交于（1，0），（3，0）两点，请写出一个满足y＜0的x的值．

答案解析收藏纠错 + 选题
14. (2019九上·西城期中) 如图，在平面直角坐标系xOy中，点A的坐标为A(1，0)，等腰直角三角形ABC的边AB在x轴的正半轴上，∠ABC=90°，点B在点A的右侧，点C在第一象限。将△ABC绕点A逆时针旋转75°，如果点C的对应点E恰好落在y轴的正半轴上，那么边AB的长为．

答案解析收藏纠错 + 选题
15. (2019九上·西城期中) 如图，抛物线C₁：y＝ $\text{[math]}$ x²经过平移得到抛物线C₂：y＝ $\text{[math]}$ x²+2x，抛物线C₂的对称轴与两段抛物线所围成的阴影部分的面积是．

答案解析收藏纠错 + 选题
16. (2019九上·西城期中) 请阅读下面材料，并回答所提出的问题．
三角形内角平分线定理：三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例．

已知：如图，△ABC中，AD是角平分线．

求证： $\text{[math]}$ ．

证明：过C作CE∥DA，交BA的延长线于E．

∴∠1＝∠E，∠2＝∠3．

∵AD是角平分线

，

∴∠1＝∠2．

∴∠3＝∠E．

∴AC＝AE．

又∵CE∥DA，

∴ $\text{[math]}$ ．……①

∴ $\text{[math]}$ ．
1. （1）上述证明过程中，步骤①处的理由是
2. （2）用三角形内角平分线定理解答：已知，△ABC中，AD是角平分线，AB＝7cm，AC＝4cm，BC＝6cm，则BD的长为cm．
答案解析收藏纠错 + 选题

三、解答题

17. (2019九上·西城期中) 如图，已知△ABC顶点的坐标分别为A（1，－1），B（4，－1），C（3，－4）．
1. （1）将△ABC绕点A逆时针旋转90°后，得到△AB₁C₁ ．在所给的直角坐标系中画出旋转后的 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标： $\text{[math]}$ ；
2. （2）以坐标原点O为位似中心，在第二象限内再画一个放大的 $\text{[math]}$ ，使得它与△ABC的位似比等于2：1 .
答案解析收藏纠错 + 选题
18. (2019九上·西城期中) 已知抛物线y＝x²+4x﹣5．
1. （1）直接写出它与x轴、y轴的交点的坐标；
2. （2）用配方法将y＝x²+4x﹣5化成y＝a(x﹣h)²+k的形式；
3. （3）抛物线y＝x²+4x﹣5是如何由抛物线y＝x²+1平移得到的．
答案解析收藏纠错 + 选题
19. (2023九上·达川月考) 如图，在矩形ABCD中，E为AD边上的一点，过C点作CF⊥CE交AB的延长线于点F．
1. （1）求证：△CDE∽△CBF；
2. （2）若B为AF的中点，CB=3，DE=1，求CD的长．
答案解析收藏纠错 + 选题
20. (2019九上·西城期中) 如图，在平面直角坐标系xOy中，抛物线y＝x²+ax+b经过点A(﹣2，0)，B(1，3)．
1. （1）求抛物线的解析式；
2. （2）由图象直接写出：x取何值时，y随x的增大而减少；
3. （3）根据图象回答：x取何值时，y＞0．
答案解析收藏纠错 + 选题
21. (2019九上·西城期中) 已知二次函数的解析式是y＝x²﹣2x﹣3．
1. （1）与y轴的交点坐标是，顶点坐标是．
2. （2）在坐标系中利用描点法画出此抛物线；
  
  x
  
  …
  
  …
  
  y
  
  …
  
  …
3. （3）结合图象回答：当﹣2＜x＜2时，函数值y的取值范围是．
答案解析收藏纠错 + 选题
22. (2020九上·金安期末) 在同车道行驶的机动车，后车应当与前车保持足以采取紧急制动措施的安全距离，如图，在一个路口，一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处，小张驾驶一辆小轿车跟随大巴车行驶．设小张距大巴车尾xm，若大巴车车顶高于小张的水平视线0.8m，红灯下沿高于小张的水平视线3.2m，若小张能看到整个红灯，求出x的最小值．

答案解析收藏纠错 + 选题
23. (2019九上·西城期中) 如图是抛物线型拱桥，当拱顶离水面8m时，水面宽AB为12m ．当水面上升6m时达到警戒水位，此时拱桥内的水面宽度是多少m？

下面给出了解决这个问题的两种方法，请补充完整：

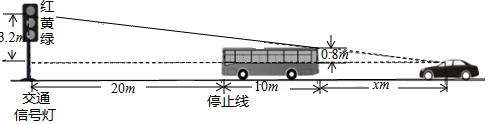
方法一：如图1，以点A为原点，AB所在直线为x轴，建立平面直角坐标系xOy ，

此时点B的坐标为（，），抛物线的顶点坐标为（，），

可求这条抛物线所表示的二次函数的解析式为．

当y＝6时，求出此时自变量x的取值，即可解决这个问题．

方法二：如图2，以抛物线顶点为原点，对称轴为y轴，建立平面直角坐标系xOy ，

这时这条抛物线所表示的二次函数的解析式为．

当y＝时，求出此时自变量x的取值为，即可解决这个问题．

答案解析收藏纠错 + 选题
24. (2019九上·西城期中) 如图，将非等腰△ABC绕点B旋转得到△DBE，且A，D，C三点在同一条直线上，BC、DE交与点O，连结EC．补全图形后，在现有图形下找出一对相似比不是1：1的相似三角形并进行证明．

答案解析收藏纠错 + 选题
25. (2019九上·西城期中) 有这样一个问题：探究函数 $\text{[math]}$ 的图象与性质．
小东根据学习函数的经验，对函数 $\text{[math]}$ 的图象与性质进行了探究．

下面是小东的探究过程，请补充完成：
1. （1）化简函数解析式，当 $\text{[math]}$ 时， $\text{[math]}$ ，当 $\text{[math]}$ 时 $\text{[math]}$ ；
2. （2）根据（1）中的结果，请在所给坐标系中画出函数 $\text{[math]}$ 的图象；备用图
3. （3）结合画出的函数图象，解决问题：若关于 $\text{[math]}$ 的方程 $\text{[math]}$ 只有一个实数根，直接写出实数a的取值范围：．
答案解析收藏纠错 + 选题
26. (2019九上·西城期中) 已知抛物线G：y＝x²﹣2ax+a﹣1（a为常数）．
1. （1）当a＝3时，用配方法求抛物线G的顶点坐标；
2. （2）若记抛物线G的顶点坐标为P（p ， q）．
  ①分别用含a的代数式表示p ， q；
  
  ②请在①的基础上继续用含p的代数式表示q；
  
  ③由①②可得，顶点P的位置会随着a的取值变化而变化，但点P总落在（）的图象上．
  
  A ．一次函数 B ．反比例函数 C ．二次函数
3. （3）小明想进一步对（2）中的问题进行如下改编：将（2）中的抛物线G改为抛物线H：y＝x²﹣2ax+N（a为常数），其中N为含a的代数式，从而使这个新抛物线H满足：无论a取何值，它的顶点总落在某个一次函数的图象上．请按照小明的改编思路，写出一个符合以上要求的新抛物线H的函数表达式：（用含a的代数式表示），它的顶点所在的一次函数图象的表达式y＝kx+b（k ， b为常数，k≠0）中，k＝，b＝．
答案解析收藏纠错 + 选题
27. (2019九上·西城期中) 如图，等腰直角三角形ABC中，∠ACB＝90°．D为射线BC上一动点．连接AD，将线段AD绕点A逆时针旋转90°至点E，连接AE、DE．点M、N分别是AB、DE的中点，连接MN．
1. （1）如图1，点D在线段BC上．
  ①猜想MN与AB的位置关系，并证明你的猜想；
  
  ②连接EB，猜想BE与BC的位置关系；
2. （2）在图2中，若点D在线段BC的延长线上，BE与BC的位置关系是否改变？请你补全图形后，证明你的猜想．
答案解析收藏纠错 + 选题
28. (2019九上·西城期中) 对某一个函数给出如下定义：若存在实数 $\text{[math]}$ ，对于任意的函数值y，都满足 $\text{[math]}$ ，则称这个函数是有界函数，在所有满足条件的M中，其最小值称为这个函数的边界值．例如，下图中的函数是有界函数，其边界值是1．
1. （1）分别判断函数 $\text{[math]}$ $\text{[math]}$ 和 $\text{[math]}$ 是不是有界函数？若是有界函数，求其边界值；
2. （2）若函数 $\text{[math]}$ $\text{[math]}$ 的边界值是2，且这个函数的最大值也是2，求b的取值范围；
3. （3）将函数 $\text{[math]}$ 的图象向下平移m个单位，得到的函数的边界值是t，当m在什么范围时，满足 $\text{[math]}$ ？
答案解析收藏纠错 + 选题