云南省昆明市西山区2019-2020学年八年级下学期数学期末...

更新时间：2024-07-13 浏览次数：243 类型：期末考试

一、填空题

1. (2023八下·长沙期中) 若式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是.

答案解析收藏纠错 + 选题
2. (2020八下·西山期末) 正比例函数 $\text{[math]}$ 经过点 $\text{[math]}$ ，则该正比例函数表达式为.

答案解析收藏纠错 + 选题
3. (2020八下·西山期末) 某运动鞋生产厂家通过市场调查得到其生产的各种尺码的运动鞋的销售量如表所示： .

鞋的尺码/ $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

销售量/双

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

根据表中数据，如果你是生产决策者，应该多生产 $\text{[math]}$ 的尺码运动鞋.

答案解析收藏纠错 + 选题
4. (2024八下·丰都县期中) 如图所示， $\text{[math]}$ 为 $\text{[math]}$ 的中位线，点F在 $\text{[math]}$ 上，且 $\text{[math]}$ ，若 $\text{[math]}$ 则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
5. (2020八上·福田期中) 直角三角形的两边长分别为5和3，该三角形的第三边的长为.

答案解析收藏纠错 + 选题
6. (2020八下·西山期末) 在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为．

答案解析收藏纠错 + 选题

二、单选题

7. (2023八下·五华期末) 下列等式成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020八下·西山期末) 由线段 $\text{[math]}$ 组成的三角形不是直角三角形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九上·开福月考) 某校八年级准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加西山区青少年科技创新大赛，各组的平时成绩的平均数 $\text{[math]}$ (单位：分)及方差 $\text{[math]}$ 如表所示：

甲

乙

丙

丁

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

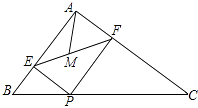
如果要选出一个成绩较好且状态稳定的组去参赛，那么应选的组是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
10. (2022八下·兴隆期末) 某通讯公司就上宽带网推出A，B，C三种月收费方式．这三种收费方式每月所需的费用y（元）与上网时间x（h）的函数关系如图所示，则下列判断错误的是（）

A . 每月上网时间不足25 h时，选择A方式最省钱 B . 每月上网费用为60元时，B方式可上网的时间比A方式多 C . 每月上网时间为35h时，选择B方式最省钱 D . 每月上网时间超过70h时，选择C方式最省钱

答案解析收藏纠错 + 选题
11. (2020八下·西山期末) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点O，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023八下·曲靖期末) 如图，已知函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，则根据图象可得不等式 $\text{[math]}$ 的解集是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2020八下·西山期末) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点A恰好落在对角线 $\text{[math]}$ 上F处，则 $\text{[math]}$ 的长是（）

A . 3 B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
14. (2020八下·西山期末) 如图， $\text{[math]}$ 的对角线 $\text{[math]}$ 交于点 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ $\text{[math]}$ 连接 $\text{[math]}$ .下列结论： $\text{[math]}$ ； $\text{[math]}$ 平分 $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ，其中正确的有（）

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

答案解析收藏纠错 + 选题

三、解答题

15. (2020八下·西山期末) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
16. (2020八下·西山期末) 已知直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点A，点A横坐标为-1，且直线 $\text{[math]}$ 与x轴交于B点，与y轴交于D点.
1. （1）求出A点的坐标及直线 $\text{[math]}$ 的解析式；
2. （2）求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
17. (2020八下·西山期末) 如图，已知点 $\text{[math]}$ 分别是 $\text{[math]}$ 的边 $\text{[math]}$ 的中点.
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）请连接 $\text{[math]}$ ，若 $\text{[math]}$ 平分 $\text{[math]}$ 试判断四边形 $\text{[math]}$ 的形状，并说明理由.
答案解析收藏纠错 + 选题

18. (2020八下·西山期末) 2020年“新冠肺炎” 预防成了所有人的首要任务，某市教育局为了晋及新冠肺炎预防知识，举办了“预防新冠，从我做起”的知识竞赛.某校初二年级有300人，现从中各随机抽取部分同学的测试成绩(每题10分，共100分)进行调查分析，并用得到的数据绘制成不完整的统计图表，如图所示：

成绩分组	频数(人数)	频率
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
合计		$\text{[math]}$

（1）统计表中的 $\text{[math]}$ ， $\text{[math]}$ ；
（2）被抽样调查的同学的竞赛成绩的众数是_分，中位数是分；
（3）请将条形图补充完整；
（4）求所有被调查同学的成绩平均分.

答案解析收藏纠错 + 选题

19. (2020八下·西山期末) 观察下列各式及其验证过程：
2 $\text{[math]}$ ，验证：2 $\text{[math]}$ ＝ $\text{[math]}$ = $\text{[math]}$ ；

3 $\text{[math]}$ ＝ $\text{[math]}$ ，验证：3 $\text{[math]}$ ＝ $\text{[math]}$ ＝ $\text{[math]}$ .
1. （1）按照上述两个等式及其验证过程的基本思路，猜想4 $\text{[math]}$ 的变形结果，并进行验证；
2. （2）写出用n(n为任意自然数，且n≥2)表示的等式反映上述各式的规律，并给出证明.
答案解析收藏纠错 + 选题
20. (2021八上·东坡期末) 小东和小明要测量校园里的一块四边形场地 $\text{[math]}$ (如图所示)的周长，其中边 $\text{[math]}$ 上有水池及建筑遮挡，没有办法直接测量其长度.小东经测量得知 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ .小明说根据小东所得的数据可以求出 $\text{[math]}$ 的长度.你同意小明的说法吗？若同意，请求出 $\text{[math]}$ 的长度；若不同意，请说明理由.

答案解析收藏纠错 + 选题
21. (2020八下·西山期末) 服务质量相同的甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.甲公司方案：每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系，如图所示.

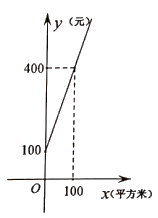
乙公司方案：绿化面积不超过 $\text{[math]}$ 平方米时，每月收取费用3000元；绿化面积超过 $\text{[math]}$ 平方米时，每月在收取 $\text{[math]}$ 元的基础上，超过的部分每平方米收取 $\text{[math]}$ 元.
1. （1）求如图所示的y与x的函数解析式； (不要求写出x的取值范围)：
2. （2）如果某学校计划投入 $\text{[math]}$ 元资金绿化校园，试通过计算说明：选择哪家公司的服务更合算.
答案解析收藏纠错 + 选题
22. (2020八下·西山期末) 如图（1），正方形 $\text{[math]}$ 的对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ 过点A作 $\text{[math]}$ 垂足为 $\text{[math]}$ 与 $\text{[math]}$ 相交于点F.
1. （1）直接写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系；
2. （2）如图（2）若点E在 $\text{[math]}$ 的延长线上， $\text{[math]}$ 于点 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点F，其他条件不变.试探究 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由.
答案解析收藏纠错 + 选题
23. (2021八下·双辽期末) 如图，四边形 $\text{[math]}$ 是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正平轴上， $\text{[math]}$ .在 $\text{[math]}$ 边上取一点D，将纸片沿 $\text{[math]}$ 翻折，使点O落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处.
1. （1）求 $\text{[math]}$ 和 $\text{[math]}$ 的长；
2. （2）求直线 $\text{[math]}$ 的表达式；
3. （3）直线 $\text{[math]}$ 与 $\text{[math]}$ 所在的直线垂直，当它与矩形 $\text{[math]}$ 有公共点时，求出b的取值范围.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

云南省昆明市西山区2019-2020学年八年级下学期数学期末...

副标题：

*注意事项：

云南省昆明市西山区2019-2020学年八年级下学期数学期末...

试题分析

总体分析

题量分析

难度分析

知识点分析

鞋的尺码/ $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
销售量/双	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$