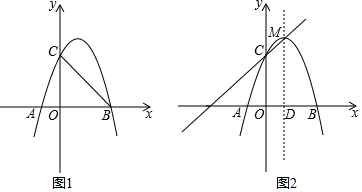浙江省宁波市海曙区2021届九年级上学期数学第一次月考试卷

更新时间：2020-12-16 浏览次数：148 类型：月考试卷

一、选择题（每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求）

1. (2020九上·海曙月考) 下列各式中，y是x的二次函数的是（　　）

A . y＝3x﹣1 B . y＝ $\text{[math]}$ C . y＝3x²+x﹣1 D . y＝2x²+ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021九上·安庆开学考) 抛物线y＝（x﹣3）²﹣5的顶点坐标是（）

A . （3，5） B . （﹣3，5） C . （3，﹣5） D . （﹣3，﹣5）

答案解析收藏纠错 + 选题
3. (2020九上·海曙月考) 关于抛物线y＝﹣x²+2x﹣3的判断，下列说法正确的是（）

A . 抛物线的开口方向向上 B . 抛物线的对称轴是直线x＝﹣1 C . 抛物线对称轴左侧部分是下降的 D . 抛物线顶点到x轴的距离是2

答案解析收藏纠错 + 选题

4. (2020九上·湖州月考) 已知二次函数y＝ax²+bx+c自变量x的部分取值和对应函数值y如表：

x	…	﹣2	﹣1	0	1	2	3	…
y	…	8	3	0	﹣1	0	3	…

则在实数范围内能使得y﹣3＞0成立的x取值范围是（　　）

A . x＞3 B . x＜﹣1 C . ﹣1＜x＜3 D . x＜﹣1或x＞3

答案解析收藏纠错 + 选题

5. (2020九上·海曙月考) 抛物线y＝2（x﹣2）²+5向左平移3个单位长度，再向下平移2个单位长度，此时抛物线的对称轴是直线（）

A . x＝2 B . x＝﹣1 C . x＝5 D . x＝0

答案解析收藏纠错 + 选题
6. (2020九上·海曙月考) 一次函数y＝acx+b与二次函数y＝ax²+bx+c在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2022九上·鹿寨期中) 已知A（0，y₁），B（1，y₂），C（4，y₃）是抛物线y＝x²﹣3x上的三点，则y₁ ， y₂ ， y₃的大小关系为（）

A . y₁＞y₂＞y₃ B . y₃＞y₁＞y₂ C . y₃＞y₂＞y₁ D . y₂＞y₁＞y₃

答案解析收藏纠错 + 选题
8. (2020九上·海曙月考) 在有22名男生和20名女生的班级中，随机抽签确定一名学生代表，则下列说法正确的是（　　）

A . 男、女生做代表的可能性一样大 B . 男生做代表的可能性较大 C . 女生做代表的可能性较大 D . 男、女生做代表的可能性的大小不能确定

答案解析收藏纠错 + 选题
9. (2020九上·海曙月考) A、B、C、D四名同学随机分为两组，两个人一组去参加辩论赛，问A、B两人恰好分到一组的概率（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021九上·于洪期中) 在一个不透明的袋子里装有若干个白球和15个黄球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过很多次重复试验，发现摸到黄球的频率稳定在0.75，则袋中白球有（）

A . 5个 B . 15个 C . 20个 D . 35个

答案解析收藏纠错 + 选题
11. (2020九上·海曙月考) 竖直上抛物体离地面的高度h（m）与运动时间t（s）之间的关系可以近似地用公式h＝﹣5t²+v₀t+h₀表示，其中h₀（m）是物体抛出时离地面的高度，v₀（m/s）是物体抛出时的速度．某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出，小球达到的离地面的最大高度为（）

A . 23.5m B . 22.5m C . 21.5m D . 20.5m

答案解析收藏纠错 + 选题
12. (2020九上·海曙月考) 如图所示，已知二次函数y＝ax²+bx+c的图象与x轴交于点A ，与y轴交于点C ， OA＝OC ，对称轴为直线x＝1，则下列结论：①abc＜0；②a+ $\text{[math]}$ ＝0；③ac+b+1＝0；④2+c是关于x的一元二次方程ax²+bx+c=0的一个根．其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每小题4分，共24分）

13. (2020九上·海曙月考) 二次函数y＝x²﹣4x+5﹣m²的图象过点（0，4），则m的值为．

答案解析收藏纠错 + 选题
14. (2024九下·南岗模拟) 如果将抛物线y=x²向上平移3个单位，那么所得新抛物线的表达式是．

答案解析收藏纠错 + 选题
15. (2020九上·海曙月考) 二次函数y＝x²﹣16x﹣8的最小值是．

答案解析收藏纠错 + 选题
16. (2020九上·海曙月考) 某彩票的中奖率是1‰，某人一次购买一盒（200张）其中每张彩票的中奖率为.

答案解析收藏纠错 + 选题
17. (2020九上·海曙月考) 小明参加“一站到底”节目，答对最后两道单选题就通关：第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．从概率的角度分析，你建议小明在第　题使用“求助”．

答案解析收藏纠错 + 选题
18. (2020九上·海曙月考) 已知二次函数y＝（m﹣2）x²+2mx+m﹣3的图象与x轴有两个交点（x₁ ， 0），（x₂ ， 0）．则下列说法正确的有：．（填序号）
①该二次函数的图象一定过定点（﹣1，﹣5）；

②若该函数图象开口向下，则m的取值范围为： $\text{[math]}$ ＜m＜2；

③当m＞2，且1≤x≤2时，y的最大值为4m﹣5；

④当m＞2，且该函数图象与x轴两交点的横坐标x₁、x₂满足﹣3＜x₁＜2，﹣1＜x₂＜0时，m的取值范围为： $\text{[math]}$ ＜m＜11．

答案解析收藏纠错 + 选题

三、解答题（本大题有8小题，共78分）

19. (2020九上·海曙月考) 一个不透明的口袋里有5个除颜色外都相同的球，其中有2个红球，3个黄球．
1. （1）若从中随意摸出一个球，求摸出红球的可能性；
2. （2）若要使从中随意摸出一个球是红球的可能性为 $\text{[math]}$ ，求袋子中需再加入几个红球？
答案解析收藏纠错 + 选题
20. (2020九上·海曙月考) 下列事件：
①从装有1个红球和2个黄球的袋子中摸出的1个球是白球；

②随意调查1位青年，他接受过九年制义务教育；

③花2元买一张体育彩票，喜中500万大奖；

④抛掷1个小石块，石块会下落．

估计这些事件的可能性大小，在相应位置填上序号．

一定会发生的事件：；发生的可能性非常大的事件：；发生的可能性非常小的事件：；不可能发生的事件：．

答案解析收藏纠错 + 选题
21. (2020九上·海曙月考) 在一个不透明的盒子里装有黑、白两种颜色的球共20只，这些球除颜色外其余完全相同，小明做摸球试验，搅匀后，他从盒子里随机摸出一只球记下颜色后，再把球放回盒子中，不断重复上述过程，如表是实验中的一组统计数据：
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
66
122
178
302
481
599
1803
摸到白球的概率 $\text{[math]}$
0.66
0.61
0.593
0.604
0.601
0.599
0.601
1. （1）请估计：当n很大时，摸到白球的频率将会接近（精确到0.1）．
2. （2）若从盒子里随机摸出一只球，则摸到白球的概率的估计值为．
3. （3）试估算盒子里黑、白两种颜色的球各有多少只？
答案解析收藏纠错 + 选题
22. (2020九上·海曙月考) 已知二次函数y＝ax²+bx﹣3的图象经过点（1，﹣4）和（﹣1，0）．
1. （1）求这个二次函数的表达式；
2. （2） x在什么范围内，y随x增大而减小？该函数有最大值还是有最小值？求这个最值．
答案解析收藏纠错 + 选题
23. (2020九上·海曙月考) 已知抛物线y＝﹣x²+2x+3．
1. （1）该抛物线的对称轴是；
2. （2）选取适当的数据填入下表，并在如图的直角坐标系内描点画出该抛物线的图象；
  
  x
  
  …
  
  -1
  
  0
  
  1
  
  2
  
  3
  
  …
  
  y
  
  …
  
  3
  
  0
  
  …
3. （3）根据函数的图象，直接写出不等式﹣x²+2x+3＞0的解．
答案解析收藏纠错 + 选题
24. (2020九上·海曙月考) 某商场购进一种每件价格为90元的新商品，在商场试销时发现：销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系.
1. （1）求出y与x之间的函数关系式；
2. （2）写出每天的利润W与销售单价x之间的函数关系式，并求出售价定为多少时，每天获得的利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
25. (2022·枣庄模拟) 如图1，抛物线y＝﹣x²+bx+c与x轴交于A、B两点，与y轴交于点C ，已知点B坐标为（3，0），点C坐标为（0，3）．
1. （1）求抛物线的表达式；
2. （2）点P为直线BC上方抛物线上的一个动点，当△PBC的面积最大时，求点P的坐标；
3. （3）如图2，点M为该抛物线的顶点，直线MD⊥x轴于点D ，在直线MD上是否存在点N ，使点N到直线MC的距离等于点N到点A的距离？若存在，求出点N的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
26. (2020九上·海曙月考) 如图，在平面直角坐标系中，抛物线y＝﹣ $\text{[math]}$ x²+bx+ $\text{[math]}$ 与x轴正半轴交于点A ，且点A的坐标为（3，0），过点A作垂直于x轴的直线l ． P是该抛物线上的任意一点，其横坐标为m ，过点P作PQ⊥l于点Q ， M是直线l上的一点，其纵坐标为﹣m+ $\text{[math]}$ ．以PQ ， QM为边作矩形PQMN ．
1. （1）求b的值．
2. （2）当点Q与点M重合时，求m的值．
3. （3）当矩形PQMN是正方形，且抛物线的顶点在该正方形内部时，求m的值．
4. （4）当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时，直接写出m的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省宁波市海曙区2021届九年级上学期数学第一次月考试卷

副标题：

*注意事项：

浙江省宁波市海曙区2021届九年级上学期数学第一次月考试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

摸球的次数n	100	200	300	500	800	1000	3000
摸到白球的次数m	66	122	178	302	481	599	1803
摸到白球的概率 $\text{[math]}$	0.66	0.61	0.593	0.604	0.601	0.599	0.601