浙江省湖州市第四中学教育集团2021届九年级上学期数学10月...

更新时间：2021-01-14 浏览次数：132 类型：月考试卷

一、选择题

1. (2020九上·射阳月考) 下列各式中，y是x的二次函数的是（）

A . y＝3x－1 B . y＝ $\text{[math]}$ C . y＝3x²＋x－1 D . y＝2x²＋ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九上·德庆期末) 下列说法正确的是（　　）

A . “经过有交通信号的路口遇到红灯”是必然事件 B . 已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次 C . 投掷一枚硬币正面朝上是随机事件 D . 明天太阳从东方升起是随机事件

答案解析收藏纠错 + 选题
3. (2021九上·安庆开学考) 抛物线y＝（x﹣3）²﹣5的顶点坐标是（）

A . （3，5） B . （﹣3，5） C . （3，﹣5） D . （﹣3，﹣5）

答案解析收藏纠错 + 选题
4. (2020九上·湖州月考) 关于抛物线y＝x²﹣6x+9，下列说法错误的是（　　）

A . 开口向上 B . 顶点在x轴上 C . 对称轴是x＝3 D . x＞3时，y随x增大而减小

答案解析收藏纠错 + 选题
5. (2020九上·湖州月考) 如图，直线y₁＝mx+n和抛物线y₂＝ax²+bx+c交于A（﹣3，1）和B （1，2）两点，使得y₁＞y₂的x的取值范围是（　　）

A . x＞1 B . x＞﹣3 C . ﹣3＜x＜1 D . x＞1或x＜﹣3

答案解析收藏纠错 + 选题
6. (2022九下·宁波开学考) 在一个不透明的盒子里有形状、大小相同的黄球2个、红球3个，从盒子里任意摸出1个球，摸到黄球的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·湖州月考) 如图，抛物线y＝x²+2x﹣1与x轴相交于A ， B两点，与y轴交于点C ，点D在抛物线上，且CD∥AB ，则线段CD的长为（　　）

A . 2 B . 3 C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题

8. (2020九上·湖州月考) 已知二次函数y＝ax²+bx+c自变量x的部分取值和对应函数值y如表：

x	…	﹣2	﹣1	0	1	2	3	…
y	…	8	3	0	﹣1	0	3	…

则在实数范围内能使得y﹣3＞0成立的x取值范围是（　　）

A . x＞3 B . x＜﹣1 C . ﹣1＜x＜3 D . x＜﹣1或x＞3

答案解析收藏纠错 + 选题

9. (2020九上·湖州月考) 在Rt△ABC中，∠C＝90°，BC＝a，AC＝b，AB＝c，若a+b＝5，则Rt△ABC的面积S关于边长c的函数关系式为（）

A . S＝ $\text{[math]}$ B . S＝ $\text{[math]}$ C . S＝ $\text{[math]}$ D . S＝ $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·铁岭模拟) 如图，抛物线y＝－x²＋2x＋m＋1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B.
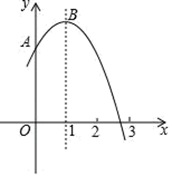
①抛物线y＝－x²＋2x＋m＋1与直线y＝m＋2有且只有一个交点；

②若点M（－2，y₁）、点N（ $\text{[math]}$ ，y₂）、点P（2，y₃）在该函数图象上，则y₁<y₂<y₃；

③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝－（x＋1）²＋m；

④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为 $\text{[math]}$ .

其中正确判断有（）

A . ①②③④ B . ②③④ C . ①③④ D . ①③

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·湖州月考) 当x=0时，函数 $\text{[math]}$ 的值为

答案解析收藏纠错 + 选题
12. (2020九上·湖州月考) 一个不透明的袋子中装有若干个红球和6个黄球，它们除颜色外都相同，从中随机摸出一个球，记下颜色后放回，通过大量反复实验发现，摸到黄球的频率约为0.3，由此推测从这个袋中摸到红球的概率约为.

答案解析收藏纠错 + 选题
13. (2020九上·湖州月考) 二次函数y＝ax²+bx+c（0≤x≤3）的图象如图所示，则y的取值范围是．

答案解析收藏纠错 + 选题
14. (2020九上·湖州月考) 斐波那契螺旋线也称为“黄金螺旋线”，是根据斐波那契数列画出来的螺旋曲线，自然界中存在许多斐波那契螺旋线国案，下列四张分别画有斐波那契螺旋线图案的卡片，它们的背面完全相同．现将它们背面朝上，从中任取一张，卡片上所画图案恰好是中心对称图形的概率是．

答案解析收藏纠错 + 选题
15. (2020九上·德保期中)
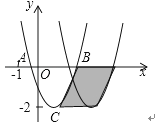
如图，已知抛物线y=ax²+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y=a₁x²+b₁x+c₁ ，则下列结论正确的是．（写出所有正确结论的序号）
①b＞0
②a﹣b+c＜0
③阴影部分的面积为4
④若c=﹣1，则b²=4a．

答案解析收藏纠错 + 选题
16. (2020九上·湖州月考) 在直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若 $\text{[math]}$ ，则称点Q为点P的“可控变点”．
例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．
1. （1）若点（﹣1，﹣2）是一次函数 $\text{[math]}$ 图象上点M的“可控变点”，则点M的坐标为；
2. （2）若点P在函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象上，其“可控变点”Q的纵坐标y′的取值范围是 $\text{[math]}$ ，则实数a的取值范围是．
答案解析收藏纠错 + 选题
17. (2020九上·湖州月考) 如图，将小球沿某方向击出时，小球的飞行路线是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t² ．
1. （1）求小球飞出1s时的飞行高度；
2. （2）求小球从飞出到落地要用的时间．
答案解析收藏纠错 + 选题
18. (2020九上·陇县期中) 已知二次函数y＝ax²+bx﹣3的图象经过点（1，﹣4）和（﹣1，0）．
1. （1）求这个二次函数的表达式；
2. （2） x在什么范围内，y随x增大而减小？该函数有最大值还是有最小值？求出这个最值．
答案解析收藏纠错 + 选题
19. (2023八下·长沙期末) 新定义：[a，b，c]为二次函数y=ax²+bx+e（a≠0，a，b，c为实数）的“图象数”，如：y=-x²+2x+3的“图象数”为[-1，2，3]
1. （1）二次函数y= $\text{[math]}$ x²-x-1的“图象数”为．
2. （2）若图象数”是[m，m+1，m+1]的二次函数的图象与x轴只有一个交点，求m的值．
答案解析收藏纠错 + 选题
20. (2020九上·湖州月考) 某单位为了创建城市文明单位，准备在单位的墙（线段MN所示）外开辟一处长方形的土地进行绿化美化，除墙体外三面要用栅栏围起来，计划用栅栏50米．
1. （1）不考虑墙体长度，问长方形的各边的长为多少时，长方形的面积最大？
2. （2）若墙体长度为20米，问长方形面积最大是多少？
答案解析收藏纠错 + 选题
21. (2020九上·北京期中) 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面
的最大距离是5m．
1. （1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（填方案一，方案二，或方案三），则B点坐标是，求出你所选方案中的抛物线的表达式；
2. （2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．
答案解析收藏纠错 + 选题
22. (2020九上·湖州月考) 假期，六盘水市教育局组织部分教师分别到A.B.C.D四个地方进行新课程培训，教育局按定额购买了前往四地的车票.如图1是未制作完成的车票种类和数量的条形统计图，请根据统计图回答下列问题：
1. （1）若去C地的车票占全部车票的30%，则去C地的车票数量是张，补全统计图.
2. （2）若教育局采用随机抽取的方式分发车票，每人一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么余老师抽到去B地的概率是多少？
3. （3）若有一张去A地的车票，张老师和李老师都想要，决定采取旋转转盘的方式来确定.其中甲转盘被分成四等份且标有数字1、2、3、4，乙转盘分成三等份且标有数字7、8、9，如图2所示.具体规定是：同时转动两个转盘，当指针指向的两个数字之和是偶数时，票给李老师，否则票给张老师（指针指在线上重转）.试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
答案解析收藏纠错 + 选题
23. (2020九上·渑池期中) 有一家苗圃计划种植桃树和柏树，根据市场调查与预测，种植桃树的利润y₁（万元）与投资成本x（万元）满足如图1所示的二次函数y₁＝ax²；种植柏树的利润y₂（万元）与投资成本x（万元）满足如图2所示的正比例函数y₂＝kx ．
1. （1）请分别直接写出利润y₁（万元）与利润y₂（万元）关于投资成本x（万元）的函数关系式；
2. （2）若这家苗圃投资4万元种植桃树，投资6万元种植柏树，则可获得的总利润是多少万元？
3. （3）若这家苗圃种植桃树和柏树投入总成本20万元，且桃树的投资成本不低于2万元，且不高于12万元，则苗圃最少能获得多少总利润？最多可获得多少总利润？
答案解析收藏纠错 + 选题
24. (2020九上·湖州月考) 如图，函数y=-x²+bx+c的图象经过点A（m ， 0），B（0，n）两点，m ， n分别是方程x²-2x-3=0的两个实数根，且m＜n ．
1. （1）求m ， n的值以及函数的解析式；
2. （2）设抛物线y=-x²+bx+c与x轴的另一交点为点C ，顶点为点D ，连结BD、BC、CD ，求△BDC面积；
3. （3）对于（1）中所求的函数y=-x²+bx+c ，
  ①当0≤x≤3时，求函数y的最大值和最小值；
  ②设函数y在t≤x≤t+1内的最大值为p ，最小值为q ，若p-q=3，求t的值．
答案解析收藏纠错 + 选题