2016年高考数学真题试卷（江苏卷）

更新时间：2016-06-14 浏览次数：767 类型：高考真卷

一、填空题：本大题共14个小题,每小题5分,共70分.请把答案写在答题卡相应位置上。

1. (2016·江苏) 已知集合A={﹣1，2，3，6}，B={x|﹣2＜x＜3}，则A∩B=.

答案解析收藏纠错 + 选题
2. (2016·江苏) 复数z=（1+2i）（3﹣i），其中i为虚数单位，则z的实部是.

答案解析收藏纠错 + 选题
3. (2020高二上·榆树期中) 在平面直角坐标系xOy中，双曲线 $\text{[math]}$ 的焦距是.

答案解析收藏纠错 + 选题
4. (2021高一下·江门月考) 已知一组数据4.7，4.8，5.1，5.4，5.5，则该组数据的方差是

答案解析收藏纠错 + 选题
5. (2019高一上·武汉月考) 函数y= $\text{[math]}$ 的定义域是.

答案解析收藏纠错 + 选题
6. (2016·江苏)
如图是一个算法的流程图，则输出的a的值是.

答案解析收藏纠错 + 选题
7. (2022高一下·佳木斯期末) 将一颗质地均匀的骰子（一种各个面上分别标有1，2，3，4，5，6个点的正方体玩具）先后抛掷2次，则出现向上的点数之和小于10的概率是.

答案解析收藏纠错 + 选题
8. (2016·江苏) 已知{a_n}是等差数列，S_n是其前n项和.若a₁+a₂²= - 3，S₅=10，则a₉的值是.

答案解析收藏纠错 + 选题
9. (2016·江苏) 定义在区间[0，3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是.

答案解析收藏纠错 + 选题
10. (2016·江苏)
如图，在平面直角坐标系xOy中，F是椭圆 $\text{[math]}$ =1（a＞b＞0）的右焦点，直线 $\text{[math]}$ 与椭圆交于B ， C两点，且∠BFC=90° ，则该椭圆的离心率是.

答案解析收藏纠错 + 选题
11. (2016·江苏) 设f（x）是定义在R上且周期为2的函数，在区间[ −1，1)上， $\text{[math]}$ 其中a∈R若 $\text{[math]}$ ，则f（5a）的值是.

答案解析收藏纠错 + 选题
12. (2016·江苏) 已知实数x ， y满足 $\text{[math]}$ ，则x²+y²的取值范围是.

答案解析收藏纠错 + 选题
13. (2016·江苏)
如图，在△ABC中，D是BC的中点，E ， F是AD上的两个三等分点， $\text{[math]}$ =4， $\text{[math]}$ =﹣1，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
14. (2016·江苏) 在锐角三角形ABC中，若sinA=2sinBsinC，则tanAtanBtanC的最小值是.

答案解析收藏纠错 + 选题

二、解答题（本大题共6小题，共90分.请在答题卡制定区域内作答，解答时应写出文字说明、证明过程或演算步骤.）

15. (2016·江苏) 在△ABC中，AC=6， $\text{[math]}$ ， $\text{[math]}$
1. （1）求AB的长；
2. （2）求cos（A﹣ $\text{[math]}$ ）的值.
答案解析收藏纠错 + 选题
16. (2016·江苏)
如图，在直三棱柱ABC﹣A₁B₁C₁中，D，E分别为AB，BC的中点，点F在侧棱B₁B上，且B₁D⊥A₁F，A₁C₁⊥A₁B₁ ．求证：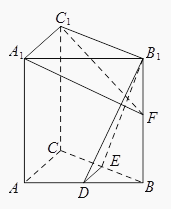
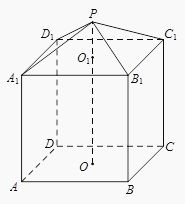
1. （1）直线DE∥平面A₁C₁F；
2. （2）平面B₁DE⊥平面A₁C1F.
答案解析收藏纠错 + 选题
17. (2016·江苏)
现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P﹣A₁B₁C₁D₁ ，下部的形状是正四棱柱ABCD﹣A₁B₁C₁D₁（如图所示），并要求正四棱柱的高O₁O是正四棱锥的高PO₁的4倍．
1. （1）若AB=6m，PO₁=2m，则仓库的容积是多少？
2. （2）若正四棱柱的侧棱长为6m，则当PO₁为多少时，仓库的容积最大？
答案解析收藏纠错 + 选题
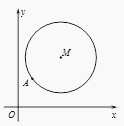
18. (2016·江苏)
如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x²+y²﹣12x﹣14y+60=0及其上一点A（2，4）．
1. （1）设圆N与x轴相切，与圆M外切，且圆心N在直线x=6上，求圆N的标准方程；
2. （2）设平行于OA的直线l与圆M相交于B、C两点，且BC=OA，求直线l的方程；
3. （3）设点T（t，0）满足：存在圆M上的两点P和Q，使得 $\text{[math]}$ ，求实数t的取值范围。
答案解析收藏纠错 + 选题
19. (2016·江苏) 已知函数f（x）=a^x+b^x（a＞0，b＞0，a≠1，b≠1）．
1. （1）设a=2，b= $\text{[math]}$ .
  ①求方程f（x）=2的根；
  ②若对于任意x∈R，不等式f（2x）≥mf（x）﹣6恒成立，求实数m的最大值；
2. （2）若0＜a＜1，b＞1，函数g（x）=f（x）﹣2有且只有1个零点，求ab的值．
答案解析收藏纠错 + 选题
20. (2016·江苏) 记U={1，2，…，100}，对数列{a_n}（n∈N^*）和U的子集T，若T=∅，定义S_T=0；若T={t₁ ， t₂ ， …，t_k}，定义S_T= $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$ ．例如：T={1，3，66}时，S_T=a₁+a₃+a₆₆ ．现设{a_n}（n∈N^*）是公比为3的等比数列，且当T={2，4}时，S_T=30．
1. （1）求数列{a_n}的通项公式；
2. （2）对任意正整数k（1≤k≤100），若T⊆{1，2，…，k}，求证：S_T＜a_k+1；
3. （3）设C⊆U，D⊆U，S_C≥S_D ，求证：S_C+S_C∩D≥2S_D ．
答案解析收藏纠错 + 选题
21. (2016·江苏) 【选做题】本题包括A、B、C、D四小题，请选定其中两小题，并在相应的答题区域内作答．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．
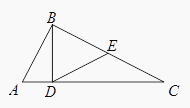
1. （1）
  A．【选修4—1几何证明选讲】
  如图，在△ABC中，∠ABC=90°，BD⊥AC ， D为垂足，E是BC的中点，求证：∠EDC=∠ABD.
2. （2） B.【选修4—2：矩阵与变换】
  已知矩阵A= $\text{[math]}$ 矩阵B的逆矩阵B^﹣¹= $\text{[math]}$ ，求矩阵AB.
3. （3）
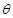  【选修4—4：坐标系与参数方程】在平面直角坐标系xOy中，已知直线l的参数方程为 $\text{[math]}$ （t为参数），椭圆C的参数方程为 $\text{[math]}$ （为参数）.设直线l与椭圆C相交于A ， B两点，求线段AB的长.
4. （4） D. 设a＞0，|x﹣1|＜ $\text{[math]}$ ，|y﹣2|＜ $\text{[math]}$ ，求证：|2x+y﹣4|＜a．
答案解析收藏纠错 + 选题
22. (2016·江苏)
如图，在平面直角坐标系xOy中，已知直线l：x-y-2=0，抛物线C：y²=2px(p＞0).
1. （1）若直线l过抛物线C的焦点，求抛物线C的方程；
2. （2）已知抛物线C上存在关于直线l对称的相异两点P和Q.
  ①求证：线段PQ的中点坐标为（2-p ， -p）；
  ②求p的取值范围.
答案解析收藏纠错 + 选题
23. (2016·江苏)
1. （1）求 $\text{[math]}$ 的值；
2. （2）
  设m ， n N^* ， n≥m ，求证：
  $\text{[math]}$ .
答案解析收藏纠错 + 选题