北京市顺义区2019-2020学年八年级上学期数学期末试卷

更新时间：2020-11-12 浏览次数：153 类型：期末考试

一、单选题

1. (2020八上·顺义期末) 如果分式 $\text{[math]}$ 值为0，那么x的值是（）

A . 0 B . 2 C . -2 D . -2或0

答案解析收藏纠错 + 选题
2. (2020八上·高阳期末) 如图所示，以BC为边的三角形共有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2020八上·顺义期末) 数轴上， $\text{[math]}$ 对应的点在（）

A . 点A、B 之间 B . 点B与C之间 C . 点C与D之间 D . 点E与F之间

答案解析收藏纠错 + 选题
4. (2021·普定模拟) 国有银行，是指由国家(财政部、中央汇金公司)直接管控的大型银行．下面是我国其中五个国有银行的图标，分别是中国工商银行、交通银行、中国农业银行、中国银行、中国建设银行，其中轴对称图形有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
5. (2020八上·顺义期末) 将 $\text{[math]}$ 分母有理化的结果为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020八上·顺义期末) 宏达公司生产了A型、B型两种计算机，它们的台数相同，但总价值和单价不同．已知A型计算机总价值为102万元；B型计算机总价值为81.6万元，且单价比A型机便宜了2400元．问A型、B型两种计算机的单价各是多少万元？对于上述问题用表格分析如下：

单价/万元

总价/万元

台数/台

A型机

M

B型机

N

如果设A型机单价为x万元，那么B型机单价为（x-0.24）万元．则标记M，N空格中的信息为（）

A . 81.6， $\text{[math]}$ B . 81.6， $\text{[math]}$ C . 102， $\text{[math]}$ D . 102， $\text{[math]}$

答案解析收藏纠错 + 选题

7. (2021·姜堰模拟) 老师组织学生做分组摸球实验．给每组准备了完全相同的实验材料，一个不透明的袋子，袋子中装有除颜色外都相同的3个黄球和若干个白球．先把袋子中的球搅匀后，从中随意摸出一个球，记下球的颜色再放回，即为一次摸球．统计各组实验的结果如下：

	一组	二组	三组	四组	五组	六组	七组	八组	九组	十组
摸球的次数	100	100	100	100	100	100	100	100	100	100
摸到白球的次数	41	39	40	43	38	39	46	41	42	38

请你估计袋子中白球的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

8. (2020八上·顺义期末) 如图，在 △ABC中，AD，AE 分别是 △ABC的角平分线和高线，用等式表示∠DAE、∠B、∠C的关系正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2020八上·顺义期末) 8的平方根是，8的立方根是.

答案解析收藏纠错 + 选题
10. (2020八上·顺义期末) 填空： $\text{[math]}$ ，则空为，．

答案解析收藏纠错 + 选题
11. (2020八上·顺义期末) 如图， $\text{[math]}$ ，那么要得到 $\text{[math]}$ ≌ $\text{[math]}$ ，可以添加一个条件是（填一个即可）， $\text{[math]}$ 与 $\text{[math]}$ 全等的理由是．

答案解析收藏纠错 + 选题
12. (2020八上·顺义期末) 若 $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2020八上·顺义期末) “任意掷一枚质地均匀的硬币，落地后正面朝上”，这个事件是事件．

答案解析收藏纠错 + 选题
14. (2020八上·顺义期末) 如图，∠C=∠ADB=90°，AD=1，BC= CD=2，则AB=.

答案解析收藏纠错 + 选题
15. (2020八上·顺义期末) 为了简洁、明确的表示一个正数的算术平方根，许多数学家进行了探索，期间经历了400余年，直至1637年法国数学家笛卡儿在他的《几何学》中开始使用“ ”表示算数平方根．我国使用根号是由李善兰（1811-1882年）译西方数学书时引用的，她在《代数备旨》中把图1所示题目翻译为： $\text{[math]}$ 则图2所示题目（字母代表正数）翻译为，计算结果为.

答案解析收藏纠错 + 选题
16. (2023八上·朝阳期中) 在 $\text{[math]}$ 中给定下面几组条件：
①BC=4cm，AC=5cm，∠ACB=30°；

②BC=4cm，AC=3cm，∠ABC=30°；

③BC=4cm，AC=5cm，∠ABC=90°；

④BC=4cm，AC=5cm，∠ABC=120°．

若根据每组条件画图，则 $\text{[math]}$ 能够唯一确定的是（填序号）.

答案解析收藏纠错 + 选题

三、解答题

17. (2020八上·顺义期末) 已知：如图，AC=BD，AC∥BD，AB和CD相交于点O．求证： $\text{[math]}$ ≌ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2020八上·顺义期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2020八上·顺义期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2020八上·顺义期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2020八上·顺义期末) 学习了分式运算后，老师布置了这样一道计算题： $\text{[math]}$ ，下面是一位同学有错的解答过程：
1. （1）该同学的解答过程的错误步骤是；（填序号）你认为该同学错误的原因是．
2. （2）请写出正确解答过程．
答案解析收藏纠错 + 选题
22. (2020八上·顺义期末) 下面是小明同学设计的“作一个角等于已知角”的尺规作图过程.
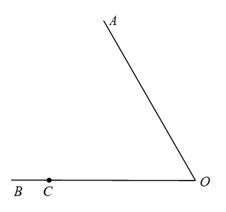
已知：∠O，

求作：一个角，使它等于∠O.

作法：如图：

①在∠O的两边上分别任取一点A，B；

②以点A为圆心，OA为半径画弧；以点B为

圆心，OB为半径画弧；两弧交于点C；

③连结AC，BC ，所以∠C即为所求作的角.

请根据小明设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下列证明．
  证明：连结AB，
  
  ∵OA=AC，OB=，，
  
  ∴ $\text{[math]}$ ≌ $\text{[math]}$ （）（填推理依据）．
  
  ∴∠C=∠O．
答案解析收藏纠错 + 选题
23. (2020八上·顺义期末) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
24. (2020八上·顺义期末) 求 $\text{[math]}$ 的值，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
25. (2022八下·凤县期中) 如图，点D，E在△ABC的边BC上，AB＝AC，AD＝AE，求证：BD＝CE.

答案解析收藏纠错 + 选题
26. (2020八上·顺义期末) 为了解某校八年级全体女生“仰卧起坐”项目的成绩，随机抽取了部分女生进行测试，并将测试成绩分为A、B、C、D四个等级，绘制成如下不完整的统计图、表.

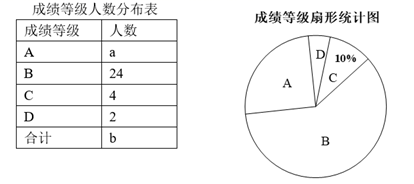
根据以上信息解答下列问题：
1. （1） a=，b= ，表示A等级扇形的圆心角的度数为度；
2. （2） A等级中有八年级（5）班两名学生，如果要从A等级学生中随机选取一名介绍“仰卧起坐”锻炼经验，求抽到八年级（5）班学生的可能性大小．
答案解析收藏纠错 + 选题
27. (2020八上·顺义期末) 在平面内，给定∠AOB=60°，及OB边上一点C，如图所示．到射线OA，OB距离相等的所有点组成图形G，线段OC的垂直平分线交图形G于点D，连接CD．
1. （1）依题意补全图形；直接写出∠DCO的度数；
2. （2）过点D作OD的垂线，交OA于点E，OB于点F．求证：CF=DE．
答案解析收藏纠错 + 选题
28. (2020八上·顺义期末) 现代科技的发展已经进入到了5G时代，“5G”即第五代移动通信技术（英语：5th generation mobile networks或5th generation wireless systems、5th-Generation，简称5G或5G技术）是最新一代蜂窝移动通信技术，也是即4G（LTE-A、WiMax）、3G（UMTS、LTE）和2G（GSM）系统之后的延伸。中国信息通信科技集团有限公司工程师余少华院士说“同4G相比，5G的传输速率提高了10至100倍．”“从人人互联、人物互联，到物物互联，再到人网物三者的结合，5G技术最终将构建起万物互联的智能世界” 如果5G网络峰值速率是4G网络峰值速率的10倍，那么在峰值速率下传输1 000MB数据，5G网络比4G网络快90秒，求这两种网络的峰值速率（MB/秒）．

答案解析收藏纠错 + 选题
29. (2022·广东模拟) 如图，在Rt $\text{[math]}$ 中，∠C=90°，AC=BC，在线段CB延长线上取一点P，以AP为直角边，点P为直角顶点，在射线CB上方作等腰 Rt $\text{[math]}$ ，过点D作DE⊥CB，垂足为点E．
1. （1）依题意补全图形；
2. （2）求证： AC=PE；
3. （3）连接DB，并延长交AC的延长线于点F，用等式表示线段CF与AC的数量关系，并证明．
答案解析收藏纠错 + 选题
30. (2020八上·顺义期末) A表示一个数，若把数A写成形如 $\text{[math]}$ 的形式，其中 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、…都为整数．则我们称把数A写成连分数形式．
例如：把2.8写成连分数形式的过程如下：

2.8-2=0.8， $\text{[math]}$ ，

1.25-1=0.25， $\text{[math]}$ ，

4-4=0．

$\text{[math]}$
1. （1）把3.245写成连分数形式不完整的过程如下：
  3.245-3=0.245， $\text{[math]}$ ，
  
  4.082-4=0.082， $\text{[math]}$ ，
  
  12.250-12=0.25， $\text{[math]}$ ，
  
  4-4=0．
  
  ∴ $\text{[math]}$
  
  则 $\text{[math]}$ ； $\text{[math]}$ ；
2. （2）请把 $\text{[math]}$ 写成连分数形式；
3. （3）有这样一个问题：如图是长为47，宽为10的长方形纸片．从中裁剪出正方形，若长方形纸片无剩余，则剪出的正方形最少是几个？
  
  小明认为这个问题和 “把一个数化为连分数形式” 有关联，并把 $\text{[math]}$ 化成连分数从而解决了问题．你可以参考小明的思路解决上述问题，请直接写出“剪出的正方形最少”时，正方形的个数．
答案解析收藏纠错 + 选题