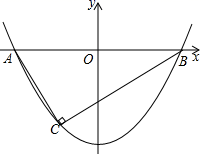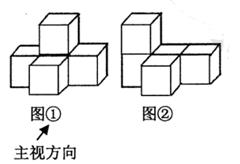
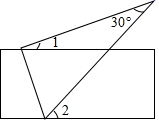
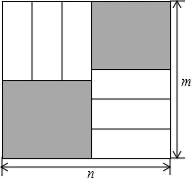
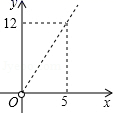
 B .
B . 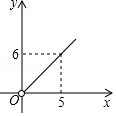 C .
C . 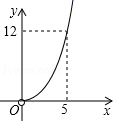 D .
D . 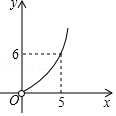
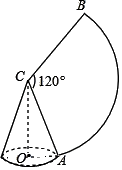
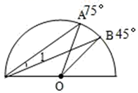
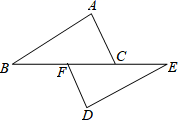
|
类别 |
家庭藏书m本 |
学生人数 |
|
A |
0≤m≤25 |
20 |
|
B |
26≤m≤50 |
a |
|
C |
51≤m≤75 |
50 |
|
D |
m≥76 |
66 |
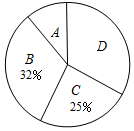
根据以上信息,解答下列问题:
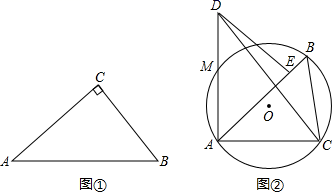
①请判断“匀称中线”是哪条边上的中线,
②求BC:AC:AB的值.