江西省吉安市吉州区2019-2020学年九年级上学期数学期末...

更新时间：2020-12-11 浏览次数：207 类型：期末考试

一、单选题

1. (2022八下·兰溪期中) 下列方程中，关于x的一元二次方程是（）

A . x²﹣x（x+3）＝0 B . ax²+bx+c＝0 C . x²﹣2x﹣3＝0 D . x²﹣2y﹣1＝0

答案解析收藏纠错 + 选题
2. (2022九上·中原期中)
如图所示的几何体的俯视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023八下·耒阳期末) 下列说法正确的是（）

A . 一组对边相等且有一个角是直角的四边形是矩形 B . 对角线互相垂直的四边形是菱形 C . 对角线相等且互相垂直的四边形是正方形 D . 对角线平分一组对角的平行四边形是菱形

答案解析收藏纠错 + 选题
4. (2022·景德镇模拟) 如图，在同一坐标系中（水平方向是x轴），函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023九上·隆昌期中) 若 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 5 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·吉州期末) 如图，菱形ABCD的边长为6，∠ABC=120°，M是BC边的一个三等分点，P是对角线AC上的动点，当PB+PM的值最小时，PM的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

7. (2024九上·平凉月考) 方程 $\text{[math]}$ 的根是.

答案解析收藏纠错 + 选题
8. (2024九下·惠阳月考) 关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个不相等的实数根，那么 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
9. (2020九上·吉州期末) 一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球个．

答案解析收藏纠错 + 选题
10. (2020九上·吉州期末) 设α，β是一元二次方程x²+3x﹣7=0的两个根，则α²+4α+β=．

答案解析收藏纠错 + 选题
11. (2023九上·杭州月考) 我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？”．其大意是：如图，一座正方形城池，A为北门中点，从点A往正北方向走30步到B处有一树木，C为西门中点，从点C往正西方向走750步到D处正好看到B处的树木，则正方形城池的边长为步．

答案解析收藏纠错 + 选题
12. (2023九上·凤翔期末)
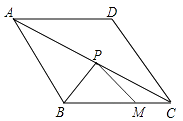
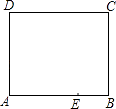
如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．

答案解析收藏纠错 + 选题

三、解答题

13. (2020九上·吉州期末) 解方程
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
14. (2020九上·吉州期末) 为落实“垃圾分类”，环卫部门要求垃圾要按A，B，C三类分别装袋，投放，其中A类指废电池，过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料，废纸等可回收垃圾．甲投放了一袋垃圾，乙投放了两袋垃圾，这两袋垃圾不同类．
1. （1）直接写出甲投放的垃圾恰好是A类的概率；
2. （2）求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率．
答案解析收藏纠错 + 选题
15. (2020九上·吉州期末)
一个直四棱柱的三视图如图所示，俯视图是一个菱形，求这个直四棱柱的表面积．

答案解析收藏纠错 + 选题
16. (2020九上·吉州期末) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 的周长之比；
2. （2）若 $\text{[math]}$ 求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2020九上·抚州期末) 如图，是由两个等边三角形和一个正方形拼在-起的图形，请仅用无刻度的直尺按要求画图，
1. （1）在图①中画一个 $\text{[math]}$ 的角，使点 $\text{[math]}$ 或点 $\text{[math]}$ 是这个角的顶点，且以 $\text{[math]}$ 为这个角的一边：
2. （2）在图②画一条直线 $\text{[math]}$ ，使得 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2020九上·吉州期末) 某单位准备组织员工到武夷山风景区旅游，旅行社给出了如下收费标准（如图所示）：

设参加旅游的员工人数为x人．
1. （1）当25＜x＜40时，人均费用元，当x≥40时，人均费用为元；
2. （2）该单位共支付给旅行社旅游费用27000元，请问这次参加旅游的员工人数共有多少人？
答案解析收藏纠错 + 选题
19. (2023八下·赣州期中) 如图，将▱ABCD的边AB延长至点E，使BE=AB，连接DE、EC、BD、DE交BC于点O．
1. （1）求证：△ABD≌△BEC；
2. （2）若∠BOD=2∠A，求证：四边形BECD是矩形．
答案解析收藏纠错 + 选题
20. (2020九上·峡江期末) 如图1是一种折叠台灯，将其放置在水平桌面上，图2是其简化示意图，测得其灯臂 $\text{[math]}$ 长为 $\text{[math]}$ 灯翠 $\text{[math]}$ 长为 $\text{[math]}$ ，底座 $\text{[math]}$ 厚度为 $\text{[math]}$ 根据使用习惯，灯臂 $\text{[math]}$ 的倾斜角 $\text{[math]}$ 固定为 $\text{[math]}$ ，
1. （1）当 $\text{[math]}$ 转动到与桌面平行时，求点 $\text{[math]}$ 到桌面的距离；
2. （2）在使用过程中发现，当 $\text{[math]}$ 转到至 $\text{[math]}$ 时，光线效果最好，求此时灯罩顶端 $\text{[math]}$ 到桌面的高度(参考数据： $\text{[math]}$ ，结果精确到个位).
答案解析收藏纠错 + 选题
21. (2020九上·吉州期末) 如图，直线y＝2x＋6与反比例函数y＝ $\text{[math]}$ (k＞0)的图像交于点A(1，m)，与x轴交于点B，平行于x轴的直线y＝n(0＜n＜6)交反比例函数的图象于点M，交AB于点N，连接BM.
1. （1）求m的值和反比例函数的表达式；
2. （2）直线y＝n沿y轴方向平移，当n为何值时，△BMN的面积最大？
答案解析收藏纠错 + 选题
22. (2020九上·吉州期末) （问题情境）
如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
1. （1）（探究展示）
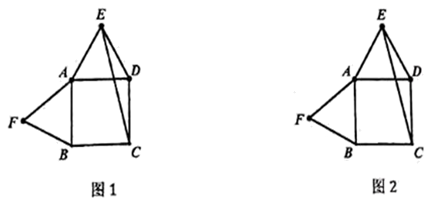
  证明：AM=AD+MC；
2. （2） AM=DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．
3. （3）（拓展延伸）
  若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．
答案解析收藏纠错 + 选题
23. (2020九上·吉州期末) 定义：有一组邻边相等的凸四边形叫做“准菱形”，利用该定义完成以下各题：
1. （1）理解：如图1，在四边形ABCD中，若（填一种情况），则四边形ABCD是“准菱形”；
2. （2）应用：证明：对角线相等且互相平分的“准菱形”是正方形；（请画出图形，写出已知，求证并证明）
3. （3）拓展：如图2，在Rt△ABC中，∠ABC=90°，AB=2，BC=1，将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF，连接AD，BF，若平移后的四边形ABFD是“准菱形”，求线段BE的长．
答案解析收藏纠错 + 选题