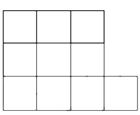
![]()


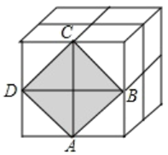
若这个正方形的边长为 ,则
=;
利用数轴可得
.
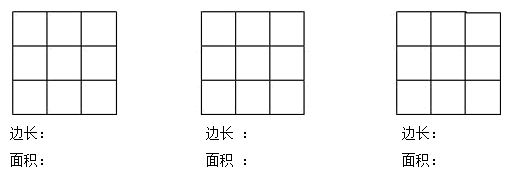

![]()
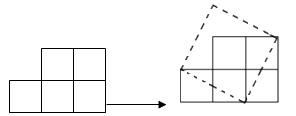
①第次滚动后,A点距离原点最近,第次滚动后,A点距离原点最远.
②当圆片结束运动时,求A点运动的路程和此时点A所表示的数.


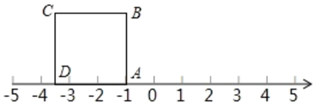
①5表示的点与数表示的点重合;
② 表示的点与数表示的点重合;
③若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是、点B表示的数是

若点M、N均为线段OC的圆周率点,求线段MN的长度.
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A , B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A , B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A , B}的奇点,但点D是{B , A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.

①当点P与点Q重合时,求t的值;
②当点P是线段AQ的三等分点时,求t的值.
材料1:我们知道在数轴上表示4和1的两点之间的距离为3(如图1),而|4﹣1|=3,所以在数轴上表示4和1的两点之间的距离为|4﹣1|.
材料2:再如在数轴上表示4和﹣2的两点之间的距离为6(如图2)而|4﹣(﹣2)|=6,所以数轴上表示数4和﹣2的两点之间的距离|4﹣(﹣2)|.

信息1:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来,比如、 、
等,而常用的“……”或者“
”的表示方法都不够百分百准确;
信息2: 的小数部分是0.5,可以看成
得来的:
信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如 ,是因为
:
根据上述信息,回答下列问题: