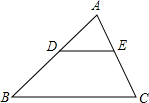
 B .
B .  C .
C .  D .
D . 
| | … | | | 0 | 1 | 2 | … |
| | … | | | | | | … |
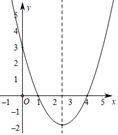
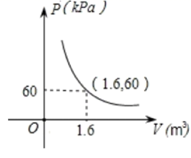
且当 时,与其对应的函数值
.有下列结论:①
;②
和3是关于
的方程
的两个根;③
.其中,正确结论的个数是( )
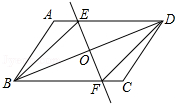


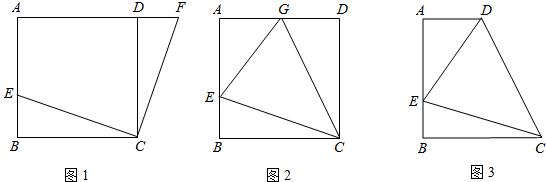
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10, 求直角梯形ABCD的面积.