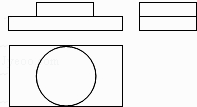
 B .
B .  C .
C .  D .
D . 
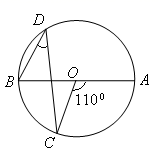

 B .
B .  C .
C .  D .
D . 
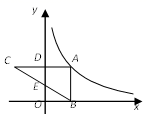

( 1 )画出△ABC关于x轴对称的△A1B1C1;
( 2 )以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1.
|
摸球的次数 |
100 |
150 |
200 |
500 |
800 |
1000 |
|
摸到白球的次数 |
58 |
96 |
116 |
295 |
484 |
601 |
|
摸到白球的频率 |
0.58 |
0.64 |
0.58 |
0.59 |
0.605 |
0.601 |


方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
