北京市丰台区2020-2021学年九年级上学期数学期中试卷

更新时间：2021-01-12 浏览次数：267 类型：期中考试

一、单选题

1. (2022九上·汝阳月考) 下面四个图形分别是绿色食品、节水、节能和回收标志，在这四个标志中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023九上·蓬江期中) 抛物线 $\text{[math]}$ 的顶点坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020九上·丰台期中) 将抛物线 $\text{[math]}$ 向左平移2个单位，再向下平移3个单位得到的抛物线是（）

A . $\text{[math]}$ B . $\text{[math]}$ ; C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020九上·周村期末) 二次函数 $\text{[math]}$ 的图象如图所示，则下列关于该函数说法中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·丰台期中) 雷达通过无线电的方法发现目标并测定它们的空间位置，因此雷达被称为“无线电定位”．现有一款监测半径为 $\text{[math]}$ 的雷达，监测点的分布情况如图，如果将雷达装置设在 $\text{[math]}$ 点，每一个小格的边长为 $\text{[math]}$ 那么能被雷达监测到的最远点为（）

A . $\text{[math]}$ 点 B . $\text{[math]}$ 点 C . $\text{[math]}$ 点 D . $\text{[math]}$ 点

答案解析收藏纠错 + 选题
6. (2023九上·贵州期末) 如图，在⊙O中，AB是直径，弦AC=5，∠BAC=∠D．则AB的长为（）

A . 5 B . 10 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·丰台期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ．在同一平面内，将 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转到 $\text{[math]}$ ，若 $\text{[math]}$ 恰好落在线段 $\text{[math]}$ 上，连接 $\text{[math]}$ ．则下列结论中错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·丰台期中) 函数 $\text{[math]}$ 的自变量 $\text{[math]}$ 的取值范围为全体实数，其中 $\text{[math]}$ 部分的图象如图所示，对于此函数有下列结论：

①函数图象关于 $\text{[math]}$ 轴对称；②函数既有最大值，也有最小值；③当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小；④当 $\text{[math]}$ 时，关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有 $\text{[math]}$ 个实数根．其中正确的结论个数是（）

A . 3 B . 2 C . 1 D . 0

答案解析收藏纠错 + 选题

二、填空题

9. (2023九上·珠海月考) 在平面直角坐标中，点 $\text{[math]}$ 关于原对称的点的坐标为．

答案解析收藏纠错 + 选题
10. (2020九上·丰台期中) 如图所示，四边形ABCD是圆内接四边形，其中 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2020九上·丰台期中) 写出一个二次函数，其图像满足：①开口向下；②与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，这个二次函数的解析式可以是．

答案解析收藏纠错 + 选题
12. (2020九上·丰台期中) 点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）.这个图案绕点O至少旋转°后能与原来的图案互相重合.

答案解析收藏纠错 + 选题
13. (2020九上·丰台期中) 如图，点P是⊙ $\text{[math]}$ 的直径BA的延长线上一点，PC切⊙ $\text{[math]}$ 于点C，若 $\text{[math]}$ ，PB=6，则PC等于．

答案解析收藏纠错 + 选题
14. (2020九上·丰台期中) 若二次函数 $\text{[math]}$ 的图象上有两点 $\text{[math]}$ ，mn．（填“＞”，“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）

答案解析收藏纠错 + 选题
15. (2020九上·北京月考) 如图，在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 的坐标分别是 $\text{[math]}$ $\text{[math]}$ 是 $\text{[math]}$ 的外接圆，则圆心 $\text{[math]}$ 的坐标为， $\text{[math]}$ 的半径为．

答案解析收藏纠错 + 选题

三、解答题

16. (2020九上·丰台期中) 在关于的 $\text{[math]}$ 二次函数中，自变量 $\text{[math]}$ 可以取任意实数，下表是自变量 $\text{[math]}$ 与函数 $\text{[math]}$ 的几组对应值：

$\text{[math]}$	…	1	2	3	4	5	6	7	8	…
$\text{[math]}$	…	-1.78	-3.70	-4.42	-3.91	-2.20	$\text{[math]}$	4.88	10.27	…

根据以上信息，关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的两个实数根中，其中的一个实数根约等于（结果保留小数点后一位）．

答案解析收藏纠错 + 选题

17. (2020九上·丰台期中) 已知二次函数 $\text{[math]}$ ．
1. （1）用配方法将其化为 $\text{[math]}$ 的形式；
2. （2）求出此二次函数的对称轴和二次函数图象与 $\text{[math]}$ 轴交点的坐标．
答案解析收藏纠错 + 选题
18. (2020九上·丰台期中) 已知一个二次函数图象上部分点的横坐标 $\text{[math]}$ 与纵坐标 $\text{[math]}$ 的对应值如下表所示：

$\text{[math]}$

…

-3

-2

-1

0

1

…

$\text{[math]}$

…

0

3

4

3

0

…
1. （1）求这个二次函数的解析式；
2. （2）在直角坐标系中画出二次函数的图象；
3. （3）结合图象，直接写出当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
19. (2020九上·丰台期中) 如图， $\text{[math]}$ 为等边三角形，将 $\text{[math]}$ 边绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到线段 $\text{[math]}$ 连接 $\text{[math]}$ ，求 $\text{[math]}$ 的度数﹒

答案解析收藏纠错 + 选题
20. (2020九上·丰台期中) 下面是“作已知三角形的高”的尺规作图过程．
已知： $\text{[math]}$ ．

求作： $\text{[math]}$ 边上的高 $\text{[math]}$ ．

作法：如图，

①分别以点 $\text{[math]}$ 和点 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径作弧，两弧相交于 $\text{[math]}$ 两点；

②作直线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，则直线 $\text{[math]}$ 是线段 $\text{[math]}$ 的 ▲ 线；

③以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作 $\text{[math]}$ ，与 $\text{[math]}$ 的延长线交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，线段 $\text{[math]}$ 即为所作的高．
1. （1）补全尺规作图并填空﹔
2. （2）判断 $\text{[math]}$ 为高的依据是．
答案解析收藏纠错 + 选题
21. (2020九上·丰台期中) 如图1所示，圆形拱门屏风是中国古代家庭中常见的装饰隔断，既美观又实用，彰显出中国元素的韵味．图2是一款拱门的示意图，其中拱门最下端 $\text{[math]}$ 分米， $\text{[math]}$ 为 $\text{[math]}$ 中点， $\text{[math]}$ 为拱门最高点，圆心 $\text{[math]}$ 在线段 $\text{[math]}$ 上， $\text{[math]}$ 分米，求拱门所在圆的半径．

答案解析收藏纠错 + 选题
22. (2020九上·丰台期中) 如图， $\text{[math]}$ 的顶点坐标分别为 $\text{[math]}$ ．
1. （1）请画出 $\text{[math]}$ 关于点 $\text{[math]}$ 成中心对称的 $\text{[math]}$ ，并写出点 $\text{[math]}$ 的坐标；
2. （2）四边形 $\text{[math]}$ 的面积为．
答案解析收藏纠错 + 选题
23. (2020九上·丰台期中) 已知二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴有公共点．
1. （1）求 $\text{[math]}$ 的取值范围；
2. （2）当 $\text{[math]}$ 为正整数时，求此时二次函数与 $\text{[math]}$ 轴的交点坐标．
答案解析收藏纠错 + 选题
24. (2021九上·大兴期中) 如图1，单孔拱桥的形状近似抛物线形，如图2建立所示的平面直角坐标系，在正常水位时，水面宽度 $\text{[math]}$ 为 $\text{[math]}$ 拱桥的最高点 $\text{[math]}$ 到水面 $\text{[math]}$ 的距离为 $\text{[math]}$ ．
1. （1）求抛物线的解析式；
2. （2）因为上游水库泄洪，水面宽度变为 $\text{[math]}$ ，求水面上涨的高度﹒
答案解析收藏纠错 + 选题
25. (2020九上·临清期末) 如图，AB为⊙O的直径，C，D是⊙O上的点，P是⊙O外一点，AC⊥PD于点E，AD平分∠BAC．
1. （1）求证：PD是⊙O的切线；
2. （2）若DE= $\text{[math]}$ ，∠BAC=60°，求⊙O的半径．
答案解析收藏纠错 + 选题
26. (2020九上·丰台期中) 在平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ ．
1. （1）抛物线 $\text{[math]}$ 的对称轴为 $\text{[math]}$ ；
2. （2）若在抛物线 $\text{[math]}$ 上有两点 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是；
3. （3）若抛物线的顶点纵坐标 $\text{[math]}$ 的取值范围为 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. (2020九上·丰台期中) 在学习利用旋转解决图形问题时，老师提出如下问题：
1. （1）如图1，点 $\text{[math]}$ 是正方形 $\text{[math]}$ 内一点， $\text{[math]}$ ，你能求出 $\text{[math]}$ 的度数吗？
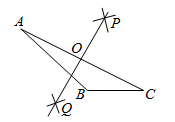
  小明通过观察、分析、思考，形成了如下思路：
  
  思路一：将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，可求出 $\text{[math]}$ 的度数；
  
  思路二：将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，可求出 $\text{[math]}$ 的度数．
  
  请参照小明的思路，任选一种写出完整的解答过程．
2. （2）如图2，若点 $\text{[math]}$ 是正方形 $\text{[math]}$ 外一点，要使 $\text{[math]}$ ，线段PA，PB，PC应满足怎样的等量关系？
  请参考小明上述解决问题的方法进行探究，直接写出线段PA，PB，PC满足的等量关系．
答案解析收藏纠错 + 选题
28. (2020九上·丰台期中) 对于平面上两点 $\text{[math]}$ ，给出如下定义：以点 $\text{[math]}$ 或 $\text{[math]}$ 为圆心， $\text{[math]}$ 长为半径的圆称为点 $\text{[math]}$ 的“共径圆”．点 $\text{[math]}$ 的“共径圆”的示意图如图所示．
1. （1）已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，则点 $\text{[math]}$ 的“共径圆”的面积为；
2. （2）已知点 $\text{[math]}$ 在以坐标原点为圆心，以 $\text{[math]}$ 为半径的圆上，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，求点 $\text{[math]}$ 的“共径圆”的半径最小值；
3. （3）已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 轴及 $\text{[math]}$ 轴上方的点，如果直线 $\text{[math]}$ 上存在两个点 $\text{[math]}$ ，使得点 $\text{[math]}$ 的“共径圆”的面积为 $\text{[math]}$ ，直接写出满足条件的 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题