浙江省台州市路桥区路桥区桐屿镇中学2021届九年级上学期数学...

更新时间：2021-03-10 浏览次数：161 类型：月考试卷

一、单选题

1. (2020九上·路桥月考) 下列图形中，只是中心对称图形而不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022八下·永年月考) 在平面直角坐标系中，若点 $\text{[math]}$ 与 $\text{[math]}$ 关于原点对称，则点 $\text{[math]}$ 在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024九下·长沙模拟) 下列说法错误的是（）

A . 必然事件发生的概率是1 B . 通过大量重复试验，可以用频率估计概率 C . 概率很小的事件不可能发生 D . 投一枚图钉，“钉尖朝上”的概率不能用列举法求得

答案解析收藏纠错 + 选题
4. (2023九上·龙马潭月考) 在同一直角坐标系中，一次函数y＝ax＋c和二次函数y＝a(x＋c)²的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2019九上·磴口期末) 如图，已知 $\text{[math]}$ ，那么下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023九上·安顺期末) 如图，正五边形 $\text{[math]}$ 内接于⊙ $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上的一点（点 $\text{[math]}$ 不与点 $\text{[math]}$ 重合），则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·靖江月考) 已知一元二次方程x²+k﹣3=0有一个根为-1，则k的值为（）

A . ﹣2 B . 2 C . ﹣4 D . 4

答案解析收藏纠错 + 选题
8. (2020九上·路桥月考) 如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时，CP的长为（）

A . 3或 $\text{[math]}$ B . 3或 $\text{[math]}$ C . 5或 $\text{[math]}$ D . 5或 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·广安期末) 我们定义一种新函数：形如 $\text{[math]}$ （a≠0，b²﹣4ac＞0）的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y＝|x²﹣2x﹣3|的图象（如图所示），并写出下列五个结论：其中正确结论的个数是（）
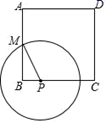
①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x＝1；③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；④当x＝﹣1或x＝3时，函数的最小值是0；⑤当x＝1时，函数的最大值是4，

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
10. (2020九上·路桥月考) 如图，在Rt△ABC 中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF.下列结论：①∠EAF=45°； ②BE=CD；③EA平分∠CEF； ④ $\text{[math]}$ ，其中正确的个数有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·路桥月考) 方程 $\text{[math]}$ 的整数解的个数是.

答案解析收藏纠错 + 选题
12. (2020九上·路桥月考) 如图，在半径为 $\text{[math]}$ 的圆形纸片中，剪一个圆心角为90°的最大扇形(阴影部分)，则这个扇形的面积为；若将此扇形围成一个无底的圆锥(不计接头)，则圆锥底面半径为。

答案解析收藏纠错 + 选题
13. (2024九下·乌鲁木齐模拟) 现有四张正面分别标有数字﹣1，1，2，3的不透明卡片，它们除数字外其余完全相同，将它们背而面朝上洗均匀，随机抽取一张，记下数字后放回，背面朝上洗均匀，再随机抽取一张记下数字，前后两次抽取的数字分别记为m ， n ，则点P（m ， n）在第二象限的概率为．

答案解析收藏纠错 + 选题
14. (2020九上·路桥月考) 对于二次函数 $\text{[math]}$ ，当自变量 $\text{[math]}$ 满足 $\text{[math]}$ 时，函数值 $\text{[math]}$ 的取值范围为 $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围为.

答案解析收藏纠错 + 选题
15. (2020九上·路桥月考) 如图，点 $\text{[math]}$ 在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转90˚到 $\text{[math]}$ 的位置，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，垂足为点 $\text{[math]}$ ，于 $\text{[math]}$ 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
16. (2020九上·路桥月考) 如图，在平面直角坐标系中，C（0，4），A（3，0），⊙A半径为2，P为⊙A上任意一点，E是PC的中点，则OE的最小值是.

答案解析收藏纠错 + 选题

三、解答题

17. (2020九上·路桥月考) 解方程
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2020九上·路桥月考) 如图所示的正方形网格中， $\text{[math]}$ 的顶点均在格点上，每个格点表示一个单位长度，请在所给直角坐标系中按要求画图和解答下列问题：
1. （1）以A点为旋转中心，将 $\text{[math]}$ 绕点A顺时针旋转90°得 $\text{[math]}$ ，画出 $\text{[math]}$
2. （2）作出 $\text{[math]}$ 关于坐标原点O成中心对称的 $\text{[math]}$
3. （3） $\text{[math]}$ 旋转得到 $\text{[math]}$ ，线段AB旋转到 $\text{[math]}$ 的过程中，线段AB扫过的面积为多少？
答案解析收藏纠错 + 选题
19. (2020九上·路桥月考) 如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上.
1. （1）求证：∠AOD=2∠E；
2. （2）若OC=3，OA=5，求AD的长.
答案解析收藏纠错 + 选题
20. (2020九上·路桥月考) 端午节吃粽子是中华民族的传统习俗，五月初五早上，奶奶为小明准备了四只粽子：一只肉馅，一只香肠馅，两只红枣馅，四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.
1. （1）请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率；
2. （2）在吃粽子之前，小明准备用一个均匀的正四面体骰子（如图所示）进行吃粽子的模拟试验，规定：掷得点数 $\text{[math]}$ 向上代表肉馅，点数2向上代表香肠馅，点数3，4向上代表红枣馅，连续抛掷这个骰子两次表示随机吃两只粽子，从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗？试说明理由.
答案解析收藏纠错 + 选题
21. (2020九上·路桥月考) 如图所示，圆 $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 与 $\text{[math]}$ 的平分线相交于点 $\text{[math]}$ ，延长 $\text{[math]}$ 交圆 $\text{[math]}$ 于点 $\text{[math]}$ ，连结 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若圆 $\text{[math]}$ 的半径为10cm， $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
22. (2020九上·路桥月考) 已知抛物线 $\text{[math]}$ 的对称轴是直线 $\text{[math]}$ ，与x轴相交于A，B两点（点B在点A右侧），与y轴交于点C.
1. （1）求抛物线的解析式和A，B两点的坐标；
2. （2）如图1，若点P是抛物线上B，C两点之间的一个动点（不与B，C重合），是否存在点P，使四边形PBOC的面积最大?若存在，求点P的坐标及四边形PBOC面积的最大值；若不存在，请说明理由；
3. （3）如图2，若点M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求点M的坐标.
答案解析收藏纠错 + 选题
23. (2020九上·路桥月考) 某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，如果每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球从发射出到第一次落在桌面的运行过程中，设乒乓球与端点A的水平距离为x（米），距桌面的高度为y（米），运行时间为t（秒），经多次测试后，得到如下部分数据：
t（秒）
0
0.16
0.2
0.4
0.6
0.64
0.8
…
x（米）
0
0.4
0.5
1
1.5
1.6
2
…
y（米）
0.25
0.378
0.4
0.45
0.4
0.378
0.25
…
1. （1）如果y是t的函数，
  ①如图，在平面直角坐标系tOy中，描出了上表中y与t各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；
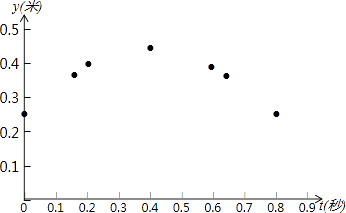
  ②当t为何值时，乒乓球达到最大高度？
2. （2）如果y是关于x的二次函数，那么乒乓球第一次落在桌面时，与端点A的水平距离是多少？
答案解析收藏纠错 + 选题
24. (2020九上·路桥月考) 某校九年级数学兴趣小组在探究相似多边形问题时，他们提出了下面两个观点：
观点一：将外面大三角形按图1的方式向内缩小，得到新三角形，它们对应的边间距都为1，则新三角形与原三角形相似.

观点二：将邻边为6和10的矩形按图2的方式向内缩小，得到新的矩形，它们对应的边间距都为1，则新矩形与原矩形相似.

请回答下列问题：
1. （1）你认为上述两个观点是否正确？请说明理由.
2. （2）如图3，已知 $\text{[math]}$ ，AC=6，BC=8，AB=10，将 $\text{[math]}$ 按图3的方式向外扩张，得到 $\text{[math]}$ ，它们对应的边间距都为1，DE=15，求 $\text{[math]}$ 的面积.
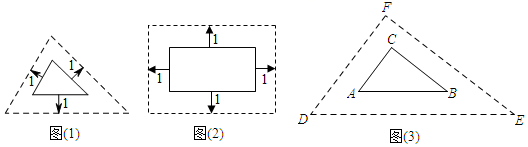
答案解析收藏纠错 + 选题