初中数学苏科版八年级下册第八章认识概率单元测试卷

更新时间：2021-03-04 浏览次数：148 类型：单元试卷

一、单选题

1. (2020八上·重庆开学考) 下列事件中，必然事件是（）

A . 随机抛掷一颗骰子，朝上的点数是6 B . 今天考试小明能得满分 C . 明天气温会升高 D . 早晨的太阳从东方升起

答案解析收藏纠错 + 选题
2. (2024八下·苏州期末) 下列说法中不正确的是（）

A . 抛掷一枚质量均匀的硬币，硬币落地时正面朝上是随机事件 B . 把4个球放入三个抽屉中，其中一个抽屉至少有两个球是必然事件 C . 为了呈现某个月的气温变化情况，应选择的统计图为扇形统计图 D . 从一副扑克牌中任意抽取1张，摸到的牌是“A”的可能性比摸到的牌是“红桃”可能性小

答案解析收藏纠错 + 选题
3. (2019八下·东台月考) 某种产品10件，其中有2件次品，其余都是正品，今从中任取一件，抽到次品的可能性为（）

A . 一定 B . 不可能 C . 可能性较大 D . 可能性较小

答案解析收藏纠错 + 选题
4. 某校八年级(1)班共有学生50人，现在对他们的生日(可以不同年)进行统计，则下列正确的说法是（）.

A . 至少有两名学生生日相同 B . 可能有两名学生生日相同 C . 不可能有两名学生生日相同 D . 肯定有两名学生生日相同

答案解析收藏纠错 + 选题
5. (2020八下·醴陵期末) 醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91--100分的为优秀,则优秀的频率是（）

分数段

61—70

71--80

81--90

91--100

人数(人)

2

8

6

4

A . 0.2 B . 0.25 C . 0.3 D . 0.35

答案解析收藏纠错 + 选题
6. (2020八下·高新期末) 一个布袋里装有4个红球、1个黄球和5个白球，除颜色外其它都相同。搅匀后任意摸出一个球，是红球的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020八下·北京期中) 设计一个摸球游戏，先在一个不透明的小盒子中放入 $\text{[math]}$ 个白球，如果希望从中任意摸出一个球，是白球的概率为 $\text{[math]}$ ，那么应该向盒子中再放入多少个其他颜色的球（游戏用球除颜色外均相同）（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023七下·砀山期末) 如图，在边长为1的小正方形网格中，△ABC的三个顶点均在格点上，若向正方形网格中投针，落在△ABC内部的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

9. (2021·姜堰模拟) 老师组织学生做分组摸球实验．给每组准备了完全相同的实验材料，一个不透明的袋子，袋子中装有除颜色外都相同的3个黄球和若干个白球．先把袋子中的球搅匀后，从中随意摸出一个球，记下球的颜色再放回，即为一次摸球．统计各组实验的结果如下：

	一组	二组	三组	四组	五组	六组	七组	八组	九组	十组
摸球的次数	100	100	100	100	100	100	100	100	100	100
摸到白球的次数	41	39	40	43	38	39	46	41	42	38

请你估计袋子中白球的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

10. (2020九上·商河期末) 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

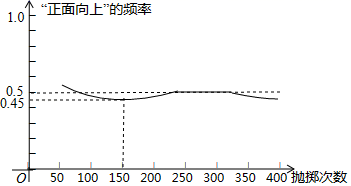
下面有三个推断：

①当抛掷次数是100时，计算机记录“正面向上”的次数是47，所以“正面向上”的概率是0.47；

②随着试验次数的增加，“正面向上”的频率总在0.5附近摆动，显示出一定的稳定性，可以估计“正面向上”的概率是0.5；

③若再次用计算机模拟此实验，则当抛掷次数为150时，“正面向上”的频率一定是0.45．

其中合理的是（　　）

A . ① B . ② C . ①② D . ①③

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·漳州月考) 袋中有5个黑球，3个白球和2个红球，每次摸一个球，摸出后再放回，在连续摸9次且9次摸出的都是黑球的情况下，第10次摸出红球的概率为．

答案解析收藏纠错 + 选题
12. (2022八下·广陵期末) 转动如图的转盘（转盘中各个扇形的面积都相等），当它停止转动时，指针指向标有数字的区域的可能性最小.

答案解析收藏纠错 + 选题
13. (2020九上·元阳期末) 某种油菜籽在相同条件下发芽试验的结果如下：

每批粒数

50

100

300

400

600

1000

发芽的频数

45

96

283

380

571

948

这种油菜籽发芽的概率的估计值是.（结果精确到0.01）

答案解析收藏纠错 + 选题
14. (2021九下·兴化月考) 一个不透明的袋子中，袋中有1 个红球，2 个白球和3 个黑球，这些球除颜色外均相同，将球摇匀后，从袋子中任意摸出一个球，摸到（填“红”或“白”或“黑”）球的可能性最大.

答案解析收藏纠错 + 选题
15. (2019八下·徐汇期末) 袋中有两个黄球、四个白球，三个绿球，它们称色外其它都一样，现从中任意出一个球，摸出绿球的概率是．

答案解析收藏纠错 + 选题
16. (2020九上·安阳期中) 在一个不透明的口袋中，有大小、形状完全相同，颜色不同的球15个，从中摸出红球的概率为 $\text{[math]}$ ，则袋中红球的个数为．

答案解析收藏纠错 + 选题
17. (2021九下·厦门开学考) 在做“抛掷一枚质地均匀的硬币”试验时，下列说法正确的是.
①不同次数的试验，正面向上的频率可能会不相同

②当抛掷的次数 $\text{[math]}$ 很大时，正面向上的次数一定为 $\text{[math]}$

③多次重复试验中，正面向上发生的频率会在某个常数附近摆动，并趋于稳定

④连续抛掷 $\text{[math]}$ 次硬币都是正面向上，第 $\text{[math]}$ 次抛掷出现正面向上的概率小于 $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2020八下·洪泽期中) 小红通过一个设有红绿灯的十字路口时遇到红灯，这是事件（填“随机”或“确定”）.

答案解析收藏纠错 + 选题
19. (2019八上·郑州开学考) 下列说法正确的是.①同角或等角的余角相等；②角是轴对称图形，角平分线是它的对称轴；③等腰三角形的平分线、底边上的中线、底边上的高重合，即“三线合一”；④必然事件发生的概率为1，不可能事件发生的概率为0.

答案解析收藏纠错 + 选题
20. (2017八下·东台期中) 在英语句子“Wish you success!”（祝你成功！）中任选一个字母，这个字母为“s”的概率为．

答案解析收藏纠错 + 选题

三、综合题

21. 在一个不透明的口袋中装有大小、外形一模一样的5个红球.3个蓝球和2个白球，它们已经在口袋中被搅匀了,请判断以下是不确定事件、不可能事件还是必然事件.
1. （1）从口袋中一次任意取出一个球,是白球.
2. （2）从口袋中一次任取5个球,全是蓝球.
3. （3）从口袋中一次任取5个球,只有蓝球和白球,没有红球.
4. （4）从口袋中一次任意取出6个球，恰好红、蓝、白三种颜色的球都齐了.
答案解析收藏纠错 + 选题
22. 一只不透明的袋子中装有1个白球、2个黄球和3个红球，每个球除颜色外都相同，将球摇匀，从中任意摸出1个球．
（1）能够事先确定摸到的球的颜色吗？
（2）你认为摸到哪种颜色的球的概率最大？
（3）改变袋子中白球、黄球、红球的个数，使摸到这三种颜色的球的概率相等．

答案解析收藏纠错 + 选题
23. (2016八上·江苏期末) 一个不透明的袋中装有20个球，其中7个黄球，8个黑球，5个红球，这些球只有颜色不同，其它都相同．
1. （1）求从袋中摸出一个球是黄球的概率；
2. （2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是 $\text{[math]}$ ，求从袋中取出黑球的个数．
答案解析收藏纠错 + 选题
24. (2015八下·泰兴期中) 一个口袋中放有16个球，其中红球6个，白球和黑球个若干个，每个球除了颜色外没有任何区别．
1. （1）小明通过大量反复的试验（每次将球搅匀后，任意摸出一个球记下颜色后再放回）发现，取出黑球的频率稳定在 $\text{[math]}$ 附近，请你估计袋中白球的个数；
2. （2）若小明取出的第一个球是白色，将它放在桌上，闭上眼睛从袋中余下的球中再任意取出一个球，取出红球的概率是多少？
答案解析收藏纠错 + 选题
25. (2015八下·淮安期中) 一只不透明的袋子中有2个红球、3个绿球和5个白球，这些球处颜色外都相同，将球搅匀，从中任意摸出1个球．
1. （1）会出现哪些可能的结果？
2. （2）能够确定摸到的一定是红球吗？
3. （3）你认为摸到哪种颜色的球可能性最大？哪种颜色的球可能性最小？
4. （4）怎样改变袋子中红球、绿球和白球的个数，使摸到这三种颜色的球的概率相同？
答案解析收藏纠错 + 选题
26. 某校师生为了对学生零花钱的使用进行教育指导，对全班50名学生每人一周内的零花钱数额进行了调查统计，并绘制如下统计表：
零花钱数额/元
5
10
15
20
学生人数/名
a
15
20
5
根据表格中信息，回答下列问题：
（1）求a的值．
（2）求着50名学生每人一周内零花钱数额的中位数．
（3）随机抽查一名学生，抽到一周内零花钱数额不大于10元的同学概率为多少？

答案解析收藏纠错 + 选题

27. (2019八下·句容期中) 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：

摸球的次数 $\text{[math]}$	100	200	300	500	800	1000	3000
摸到白球的次数 $\text{[math]}$	65	124	278	302	481	599	1803
摸到白球的频率 $\text{[math]}$	0.65	0.62	0.593	0.604	0.601	0.599	0.601

（1）请估计当 $\text{[math]}$ 很大时，摸到白球的频率将会接近（精确到0.1）；
（2）假如摸一次，摸到黑球的概率 $\text{[math]}$ ；
（3）试估算盒子里黑颜色的球有多少只.

答案解析收藏纠错 + 选题

28. (2017八下·南京期中) 在一个不透明的口袋里装有若干个相同的红球，为了用估计袋中红球的数量，八（9）班学生在数学实验室分组做摸球实验：每组先将10个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复．下表是这次活动统计汇总各小组数据后获得的全班数据统计表：
1. （1）按表格数据格式，表中的a=；b=；
2. （2）请估计：当次数s很大时，摸到白球的频率将会接近；
3. （3）请推算：摸到红球的概率是（精确到0.1）；
4. （4）试估算：口袋中红球有多少只？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

初中数学苏科版八年级下册第八章认识概率单元测试卷

副标题：

*注意事项：

初中数学苏科版八年级下册第八章认识概率单元测试卷

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

每批粒数	50	100	300	400	600	1000
发芽的频数	45	96	283	380	571	948

分数段	61—70	71--80	81--90	91--100
人数(人)	2	8	6	4

零花钱数额/元	5	10	15	20
学生人数/名	a	15	20	5

小学

初中

高中

初中数学苏科版八年级下册第八章 认识概率 单元测试卷

副标题：

*注意事项：

初中数学苏科版八年级下册第八章 认识概率 单元测试卷

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

初中数学苏科版八年级下册第八章认识概率单元测试卷

初中数学苏科版八年级下册第八章认识概率单元测试卷