初中数学湘教版七年级下册第二章整式的乘法单元测试（提高篇...

更新时间：2021-03-07 浏览次数：194 类型：单元试卷

一、单选题

1. (2020七下·覃塘期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . -64 B . -48 C . 48 D . 64

答案解析收藏纠错 + 选题
2. (2020七下·杭州期末) 我们知道：若a^m＝aⁿ（a＞0且a≠1），则m＝n.设5^m＝3，5ⁿ＝15，5^p＝75.现给出m，n，p三者之间的三个关系式：①m+p＝2n；②m+n＝2p﹣1；③n²﹣mp＝1.其中正确的是（）

A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题
3. (2020七下·孝感期中) 已知多项式 $\text{[math]}$ 的积中x的一次项系数为零，则m的值是（）

A . 1 B . –1 C . –2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020七下·温州期末) 如图所示，以长方形 $\text{[math]}$ 的各边为直径向外作半圆，若四个半圆的周长之和为 $\text{[math]}$ ，面积之和为 $\text{[math]}$ ，则长方形 $\text{[math]}$ 的面积为（）

A . 10 B . 20 C . 40 D . 80

答案解析收藏纠错 + 选题
5. (2021九上·镇平月考) 已知 M = a² - a ， N = a -1（ a 为任意实数），则 M 、 N 的大小关系为（）

A . M＞ N B . M≥N C . M＜ N D . M≤ N

答案解析收藏纠错 + 选题
6. (2020七下·郏县期末) 通过计算几何图形的面积可表示一些代数恒等式，小明从图中得到 $\text{[math]}$ 个代数恒等式：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ 其中正确的有（）

A . ②③ B . ①②③ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
7. (2020七下·枣庄期中) 已知实数 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ，则a-b的值为（）

A . 6 B . -6 C . 14 D . -14

答案解析收藏纠错 + 选题
8. 如果四个互不相同的正整数m，n，p，q满足(6-m)(6-n)(6-p)(6-q)=4，那么m+n+p+q=(　　)

A . 24　　　　 B . 25　　　　　 C . 26　　　 D . 28

答案解析收藏纠错 + 选题
9. (2019七下·漳州期末) 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 $\text{[math]}$ 为非负整数）的展开式中，把各项系数按一定的规律排成右表（展开后每一项按 $\text{[math]}$ 的次数由大到小的顺序排列）．人们把这个表叫做“杨辉三角”．据此规律，则 $\text{[math]}$ 展开式中含 $\text{[math]}$ 项的系数是 $\text{[math]}$ 　　 $\text{[math]}$

A . 2016 B . 2017 C . 2018 D . 2019

答案解析收藏纠错 + 选题
10. (2020七下·郑州期末) 如图，有两个正方形A ， B ，现将B放在A的内部得图甲，将A ， B并列放置后构造新的正方形得图乙。若图甲和图乙中阴影部分的面积分别为3和30，则正方形A、B的面积之和为（）

A . 33 B . 30 C . 27 D . 24

答案解析收藏纠错 + 选题
11. (2019七下·兰州月考) 观察下列各式及其展开式：（）
$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

……

你猜想 $\text{[math]}$ 的展开式第三项的系数是（）

A . 66 B . 55 C . 45 D . 36

答案解析收藏纠错 + 选题
12. 不论x、y为什么实数，代数式x²+y²+2x﹣4y+7的值（）

A . 总不小于2 B . 总不小于7 C . 可为任何实数 D . 可能为负数

答案解析收藏纠错 + 选题

二、填空题

13. (2024七上·义乌月考) 观察下列各数，按照某种规律在横线上填上一个适当的数。
$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，.

答案解析收藏纠错 + 选题
14. (2020七下·昌平期末) 观察、归纳：
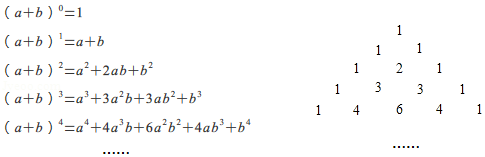
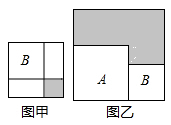
（x﹣1）（x+1）＝x²﹣1；

（x﹣1）（x²+x+1）＝x³﹣1；

（x﹣1）（x³+x²+x+1）＝x⁴﹣1；

…

请你根据以上等式的规律，完成下列问题：

⑴（x﹣1）（xⁿ+…+x²+x+1）＝﹣1；

⑵计算：1+2+2²+…+2²⁰¹⁹＝．

答案解析收藏纠错 + 选题
15. (2019七下·顺德月考) $\text{[math]}$ 的个位数字是．

答案解析收藏纠错 + 选题
16. 一个自然数若能表示为两个自然数的平方差，则这个自然数称为“智慧数”．比如：2²-1²=3，则3就是智慧数；2²-0²=4，则4就是智慧数．
从0开始第7个智慧数是；不大于200的智慧数共有．

答案解析收藏纠错 + 选题
17. (2010·华罗庚金杯竞赛) 在2001、2002、…、2010这10个数中，不能表示成两个平方数差的数有个。

答案解析收藏纠错 + 选题
18. (2019七下·涡阳期末) 已知a²+ab+b²=7，a²-ab+b²=9，则（a+b）²=．

答案解析收藏纠错 + 选题

三、解答题

19. 用乘法公式计算下列各式的值
1. （1） $\text{[math]}$
2. （2） (2+1)(2²+1)(2⁴+1)⋯(2²ⁿ+1)
答案解析收藏纠错 + 选题
20. 计算：（a－b）^2m-1·（b－a）^2m·（a－b）^2m+1 ，其中m为正整数．

答案解析收藏纠错 + 选题
21. 证明：两个连续奇数的平方差是8的倍数，并且等于这两个数的和的两倍．

答案解析收藏纠错 + 选题
22. (2020七上·林西期末) 阅读探究，理解应用，根据乘方的意义填空，并思考：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
3. （3） $\text{[math]}$ （m，n是正整数）
  一般地，对于任意底数a与任意正整数m，n，则有： $\text{[math]}$
  
  根据你发现的规律，完成下列问题：
  
  计算： $\text{[math]}$ ； $\text{[math]}$ ；
  
  $\text{[math]}$ ；
4. （4）已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2020七上·长春期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ ， $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ．
2. （2）当 $\text{[math]}$ ， $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ ．
3. （3）观察（1）和（2）的结果，可以得出结论： $\text{[math]}$ （n为正整数）．
4. （4）此性质可以用来进行积的乘方运算，反之仍然成立．如 $\text{[math]}$ ， $\text{[math]}$ ，…．应用上述等式，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2020八上·泉州月考) 好学小东同学，在学习多项式乘以多项式时发现：( $\text{[math]}$ x+4)(2x+5)(3x-6)的结果是一个多项式，并且最高次项为： $\text{[math]}$ x•2x•3x＝3x³ ，常数项为：4×5×(-6)=-120，那么一次项是多少呢？要解决这个问题，就是要确定该一次项的系数．根据尝试和总结他发现：一次项系数就是： $\text{[math]}$ ×5×(-6)+2×(-6)×4+3×4×5＝-3，即一次项为-3x ．
请你认真领会小东同学解决问题的思路，方法，仔细分析上面等式的结构特征．结合自己对多项式乘法法则的理解，解决以下问题．
1. （1）计算(x+2)(3x+1)(5x-3)所得多项式的一次项系数为．
2. （2） ( $\text{[math]}$ x+6)(2x+3)(5x-4)所得多项式的二次项系数为．
3. （3）若计算(x²+x+1)(x²-3x+a)(2x-1)所得多项式不含一次项，求a的值；
4. （4）若(x+1)²⁰²¹=a₀x²⁰²¹+a₁x²⁰²⁰+a₂x²⁰¹⁹+···+a₂₀₂₀x+a₂₀₂₁ ，则a₂₀₂₀=．
答案解析收藏纠错 + 选题
25. (2020七下·新昌期末) 某同学利用若干张正方形纸片进行以下操作：
1. （1）从边长为a的正方形纸片中减去一个边长为b的小正方形，如图1，再沿线段AB把纸片剪开，最后把剪成的两张纸片拼成如图2的等腰梯形，这一过程所揭示的公式是.
2. （2）先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出两张边长分别为a和b的长方形纸片，如图3，最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式？
3. （3）先剪出两个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出三张边长分别为a和占的长方形纸片，如图5，你能否把图5中所有纸片拼成一个长方形？
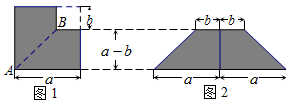
  如果可以，请画出草图，并写出相应的等式.如果不能，请说明理由.
答案解析收藏纠错 + 选题
26. (2019七下·合肥期中) 阅读材料：如果一个数的平方等于﹣1，记为i²＝﹣1，这个数i叫做虚数单位，那么形如a+bi（a ， b为实数）的数就叫做复数，a叫这个复数的实部，b叫做这个复数的虚部．它有如下特点：
①它的加，减，乘法运算与整式的加，减，乘法运算类似例如计算：

（2+i）+（3﹣4i）＝（2+3）+（1﹣4）i＝5﹣3i；（3+i）i＝3i+i²＝3i﹣1

②若他们的实部和虚部分别相等，则称这两个复数相等若它们的实部相等，虚部互为相反数，则称这两个复数共轭，如1+2i的共轭复数为1﹣2i ．
1. （1）填空：（3i﹣2）（3+i）＝；（1+2i）³（1﹣2i）³＝；
2. （2）若a+bi是（1+2i）²的共轭复数，求（b﹣a）^a的值；
3. （3）已知（a+i）（b+i）＝1﹣3i ，求（a²+b²）（i²+i³+i⁴+…+i²⁰¹⁹）的值．
答案解析收藏纠错 + 选题