北京市顺义区2020-2021学年九年级上学期数学期末试卷

更新时间：2021-03-31 浏览次数：181 类型：期末考试

一、单选题

1. (2020九上·顺义期末) 数轴上A、B、C、D四个点的位置如图所示，这四个点中，表示2的相反数的点是（）

A . 点 A B . 点B C . 点C D . 点D

答案解析收藏纠错 + 选题
2. 如果 $\text{[math]}$ （ $\text{[math]}$ ），那么下列比例式中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·杭州模拟) 在Rt△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则tanB的值为（）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020九上·顺义期末) 将抛物线 $\text{[math]}$ 向下平移1个单位，得到的抛物线是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·顺义期末) 如图，在△ABC中，D、E分别是边AB、AC上的点，且DE∥BC，若AD：DB＝2：3，则△ADE与△ABC的面积比等于（）

A . 2：3 B . 4：5 C . 4：9 D . 4：25

答案解析收藏纠错 + 选题
6. (2020九上·顺义期末) 二次函数的图象如图所示，则这个二次函数的表达式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·顺义期末) 如图，点A，B，C都在⊙O上，若∠AOC=140°，则∠B的度数是（）

A . 70° B . 80° C . 110° D . 140°

答案解析收藏纠错 + 选题
8. (2023九上·霞山月考) 已知抛物线 $\text{[math]}$ 上部分点的横坐标x与纵坐标y的对应值如下表：

$\text{[math]}$

…

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

0

…

$\text{[math]}$

…

$\text{[math]}$

$\text{[math]}$

1

0

$\text{[math]}$

…

有以下几个结论：

①抛物线 $\text{[math]}$ 的开口向上；

②抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ；

③关于x的方程 $\text{[math]}$ 的根为 $\text{[math]}$ 和 $\text{[math]}$ ；

④当y＜0时，x的取值范围是 $\text{[math]}$ ＜x＜ $\text{[math]}$ ．

其中正确的是（）

A . ①④ B . ②④ C . ②③ D . ③④

答案解析收藏纠错 + 选题

二、填空题

9. (2024九上·克东开学考) 方程组 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
10. (2020九上·顺义期末) 一个圆柱体容器内装入一些水，截面如图所示，若⊙O中的直径为52cm，水面宽AB＝48cm，则水的最大深度为cm．

答案解析收藏纠错 + 选题
11. (2020九上·顺义期末) 小明为了测量一个小湖泊两岸的两棵树A、B之间的距离，在垂直AB的方向BC上确定点C，测得BC＝45m，∠C＝40°，从而计算出AB之间的距离．则AB＝．（精确到0.1m）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

答案解析收藏纠错 + 选题
12. (2020九上·顺义期末) 如图，在⊙O中，若弧AB＝BC＝CD，则AC与2CD的大小关系是：AC2CD．（填“＞”，“＜”或“＝”）

答案解析收藏纠错 + 选题
13. (2020九上·顺义期末) 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，AB＝9，AC＝6，则cos∠DCB ＝．

答案解析收藏纠错 + 选题
14. (2020九上·顺义期末) 如图，小明抛投一个沙包，沙包被抛出后距离地面的高度h（米）和飞行时间t（秒）近似满足函数关系式 $\text{[math]}$ ，则沙包在飞行过程中距离地面的最大高度是米．

答案解析收藏纠错 + 选题
15. (2020九上·顺义期末) 在反比例函数 $\text{[math]}$ 的图象上有两点A（x₁ ， y₁），B（x₂ ， y₂），且x₁＜ x₂＜0，y₁＞ y₂写出一个符合条件的函数表达式．

答案解析收藏纠错 + 选题
16. (2020九上·顺义期末) 如图，线段AB＝9，AC⊥AB于点A，BD⊥AB于点B，AC＝2，BD＝4，点P为线段AB上一动点，且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似，则AP的长为．

答案解析收藏纠错 + 选题

三、解答题

17. (2021·西安模拟) 解不等式组： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2020九上·顺义期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2020九上·顺义期末) 已知：如图，点M为锐角∠APB的边PA上一点．
求作：∠AMD，使得点D在边PB上，且∠AMD ＝2∠P．

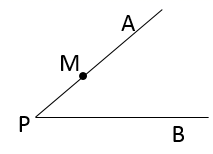
作法：①以点M为圆心，MP长为半径画圆，交PA于另一点C，交PB 于点D点；

②作射线MD．
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
  证明：∵P、C、D都在⊙M上，
  
  ∠P为弧CD所对的圆周角，∠CMD为弧CD所对的圆心角，
  
  ∴∠P＝ $\text{[math]}$ ∠CMD（）（填推理依据）．
  
  ∴∠AMD ＝2∠P．
答案解析收藏纠错 + 选题
20. (2020九上·顺义期末) 已知：如图，△ABC∽△ACD，CD平分∠ACB，AD ＝2，BD ＝3，求AC、DC的长．

答案解析收藏纠错 + 选题
21. (2020九上·顺义期末) 一艘船向正北方向航行，在A处时看到灯塔S在船的北偏东30°的方向上，继续航行12海里到达B处，看到灯塔S在船的北偏东60°的方向上．若继续沿正北方向航行，求航行过程中船距灯塔S的最近距离．（结果精确到0.1海里）（参考数据： $\text{[math]}$ ≈1.41， $\text{[math]}$ ≈1.73）

答案解析收藏纠错 + 选题
22. (2020九上·顺义期末) 已知： AB为⊙O的直径，点D为弧BC的中点，过点D作⊙O的切线交AB的延长线于点E，连接CB．
1. （1）求证：BC∥DE；
2. （2）若cosE＝ $\text{[math]}$ ， DE ＝20，求BC的长．
答案解析收藏纠错 + 选题
23. (2020九上·顺义期末) 在平面直角坐标系xOy中，有抛物线 $\text{[math]}$ （ $\text{[math]}$ ）．
1. （1）求抛物线的顶点坐标（用含m的式子表示）；
2. （2）过点A（0，1）作y轴的垂线l，点B在直线l上且横坐标是2m＋1
  ①若m的值等于1，求抛物线与线段AB的交点个数；
  
  ②若抛物线与线段AB只有一个公共点，直接写出m的取值范围．
答案解析收藏纠错 + 选题
24. (2020九上·顺义期末) 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D为线段BC上一动点（不与点B， C重合），作射线AD、AB，将射线AD、AB分别绕点A顺时针旋转90°，得到射线 $\text{[math]}$ ， $\text{[math]}$ ，过点B作BC的垂线，分别交射线 $\text{[math]}$ ， $\text{[math]}$ 于点E，F．
1. （1）依题意补全图形；
2. （2）求证：AB＝AF；
3. （3）用等式表示线段AC，BD与BE之间的数量关系，并证明．
答案解析收藏纠错 + 选题
25. (2020九上·顺义期末) 在平面直角坐标系xOy中，对于点P，若点Q满足条件：以线段PQ为对角线的正方形，边均与某条坐标轴垂直，则称点Q为点P的“正轨点”，该正方形为点P的“正轨正方形”如下图所示．
1. （1）已知点A的坐标是（1，3）．
  ①在（－3，－1），（2，2），（3，3）中，是点A的“正轨点”的坐标是．
  
  ②若点A的“正轨正方形”的面积是4，写出一个点A的“正轨点”的坐标：
2. （2）若点B（1，0）的“正轨点”在直线y＝2x＋2上，求点B的“正轨点”的坐标；
3. （3）已知点C（m，0），若直线y＝2x＋m上存在点C的“正轨点”，使得点C的“正轨正方形”面积小于4，直接写出m的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

北京市顺义区2020-2021学年九年级上学期数学期末试卷

副标题：

*注意事项：

北京市顺义区2020-2021学年九年级上学期数学期末试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	0	…
$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	1	0	$\text{[math]}$	…