B .
B .  C .
C . 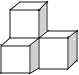 D .
D . 
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 185 | 180 | 185 | 180 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为.
在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
|
5640 |
6430 |
6520 |
6798 |
7325 |
|
8430 |
8215 |
7453 |
7446 |
6754 |
|
7638 |
6834 |
7326 |
6830 |
8648 |
|
8753 |
9450 |
9865 |
7290 |
7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
|
组别 |
步数分组 |
频数 |
|
A |
5500≤x<6500 |
2 |
|
B |
6500≤x<7500 |
10 |
|
C |
7500≤x<8500 |
m |
|
D |
8500≤x<9500 |
3 |
|
E |
9500≤x<10500 |
n |
请根据以上信息解答下列问题:

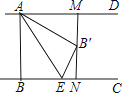
如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … | |
y | … | 3 | m | ﹣1 | 0 | ﹣1 | 0 | 3 | … |
其中,m=.
①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是.
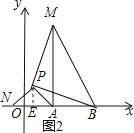
当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)
应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.