2016年江苏省苏州市中考数学试卷

如图，直线a∥b，直线l与a、b分别相交于A、B两点，过点A作直线l的垂线交直线b于点C，若∠1=58°，则∠2的度数为（　　）

则这30户家庭该用用水量的众数和中位数分别是（　　）

如图，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为（　　）

矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在AB上，当△CDE的周长最小时，点E的坐标为（　　）

如图，在四边形ABCD中，∠ABC=90°，AB=BC=2 ，E、F分别是AD、CD的中点，连接BE、BF、EF．若四边形ABCD的面积为6，则△BEF的面积为（　　）

某学校计划购买一批课外读物，为了了解学生对课外读物的需求情况，学校进行了一次“我最喜爱的课外读物”的调查，设置了“文学”、“科普”、“艺术”和“其他”四个类别，规定每人必须并且只能选择其中一类，现从全体学生的调查表中随机抽取了部分学生的调查表进行统计，并把统计结果绘制了如图所示的两幅不完整的统计图，则在扇形统计图中，艺术类读物所在扇形的圆心角是度．

如图，AB是⊙O的直径，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若∠A=∠D，CD=3，则图中阴影部分的面积为．

如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接AB′，则AB′的长为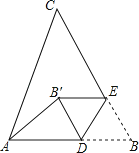

如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2 ），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线第一次垂直时，点P的坐标为

解不等式2x﹣1＞ ，并把它的解集在数轴上表示出来．

在一个不透明的布袋中装有三个小球，小球上分别标有数字﹣1、0、2，它们除了数字不同外，其他都完全相同．

如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E．

如图，一次函数y=kx+b的图象与x轴交于点A，与反比例函数y= （x＞0）的图象交于点B（2，n），过点B作BC⊥x轴于点C，点P（3n﹣4，1）是该反比例函数图象上的一点，且∠PBC=∠ABC，求反比例函数和一次函数的表达式．

如图，AB是⊙O的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD=BD，连接AC交⊙O于点F，连接AE、DE、DF．

如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3m/s，以O为圆心，0.8cm为半径作⊙O，点P与点O同时出发，设它们的运动时间为t（单位：s）（0＜t＜ ）．

如图，直线l：y=﹣3x+3与x轴、y轴分别相交于A、B两点，抛物线y=ax²﹣2ax+a+4（a＜0）经过点B．