B .
B .  C .
C .  D .
D . 
 B .
B . 
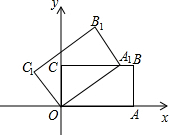
① ;②
>
;③若n>m>0,则
时的函数值小于
时的函数值;④点(
,0)一定在此抛物线上.
其中正确结论的个数是( )
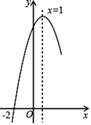
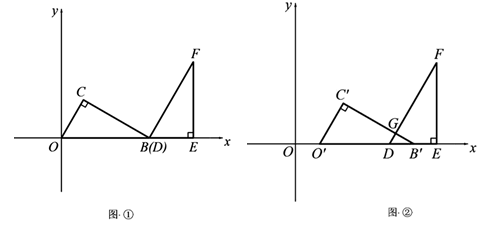
(Ⅰ)当点E为CD边的中点时,求△ABF的面积为;
(Ⅱ)当DP+PF最短时,请在图2所示的网格中,用无刻度的直尺画出点P , 并简要说明点P的位置是如何找到的(不要求证明).
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ▲ ;
(Ⅱ)解不等式②,得 ▲ ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 ▲ .
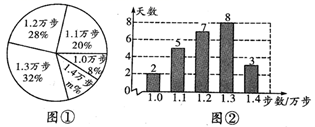
(Ⅰ)本次记录的总天数为 ▲ , 图①中m的值为 ▲ ;
(Ⅱ)求小名近期健步走步数的平均数、众数和中位数;
(Ⅲ)根据样本数据,若小明坚持健步走一年(记为365天),试估计步数为1.1万步的天数.

参考数据: ,
,
,
.
A公司方案:无纺布的价格均为每吨1.95万元 ;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
设甲厂在同一公司一次购买无纺布的数量为x吨(x>0).
(Ⅰ)根据题意,填写下表:
| 一次购买数量(吨) | 10 | 20 | 35 | … |
| A公司花费(万元) | 39 | … | ||
| B公司花费(万元) | 40 | … |
(Ⅱ)设在A公司花费 万元,在B公司花费
万元,分别求
、
关于x的函数解析式;
(Ⅲ)如果甲厂所需购买的无纺布是50吨,试通过计算说明选择哪家公司费用较少.