江苏省南京市秦淮区2021届九年级上学期数学期末考试试卷

更新时间：2021-05-25 浏览次数：161 类型：期末考试

一、单选题

1. (2023九上·梁溪期中) 下列方程是一元二次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021九上·秦淮期末) 下列随机事件：①在一副扑克牌中，抽一张是红桃；②抛掷一枚质地均匀的骰子，朝上一面是偶数；③抛一枚质地均匀的硬币，正面朝上；④不透明的袋子中有除颜色外完全相同的红球和白球各2个，摸出一个是白球，其中，概率为 $\text{[math]}$ 的是（）

A . ①③ B . ①②③ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题
3. (2021九上·秦淮期末) 圆锥的底面半径为2，母线长为4，则其侧面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九上·秦淮期末) 某排球队6名场上队员的身高（单位：cm）是180，184，188，190，190，194.现用两名身高分别为185cm和188cm的队员换下场上身高为184cm和190cm的队员.与换人前相比，场上队员的身高（）

A . 平均数变小，众数变小 B . 平均数变小，众数变大 C . 平均数变大，众数变小 D . 平均数变大，众数变大

答案解析收藏纠错 + 选题
5. (2021九上·秦淮期末) 关于x的方程 $\text{[math]}$ （p为常数）的根的情况，下列结论中正确的是（）

A . 两个正根 B . 两个负根 C . 一个正根，一个负根 D . 根的符号与p的值有关

答案解析收藏纠错 + 选题
6. (2021九上·秦淮期末) 已知四边形ABCD，下列命题：①若 $\text{[math]}$ ，则四边形ABCD一定存在外接圆；②若四边形ABCD内存在一点到四个顶点的距离相等，则 $\text{[math]}$ ；③若四边形ABCD内存在一点到四条边的距离相等，则 $\text{[math]}$ ，其中，真命题的个数为（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空题

7. (2020九上·南京期中) 方程x²﹣4＝0的解是．

答案解析收藏纠错 + 选题
8. (2024九下·哈尔滨模拟) 若扇形的圆心角为60°，弧长为2π，则扇形的半径为．

答案解析收藏纠错 + 选题
9. (2021九上·秦淮期末) 将一元二次方程 $\text{[math]}$ 变形为 $\text{[math]}$ 的形式为.

答案解析收藏纠错 + 选题

10. (2021九上·秦淮期末) 甲、乙两名射击运动员在平时某练习中的成绩如下表：

甲的成绩					乙的成绩
环数	7	8	9	10	环数	7	8	9	10
频数	2	3	3	2	频数	4	6	6	4

则甲、乙两名射击运动员在该练习中成绩的方差 $\text{[math]}$ 、 $\text{[math]}$ 的大小关系为.

答案解析收藏纠错 + 选题

11. (2021九上·铅山期末) 如图，在圆内接四边形ABCD中， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的度数之比为 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2021九上·秦淮期末) 如图，在平面直角坐标系中，一个圆经过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点，则该圆的圆心的坐标是.

答案解析收藏纠错 + 选题
13. (2024九上·罗平期中) $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的一个根， $\text{[math]}$ ，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
14. (2021九上·秦淮期末) 某商店将进价为30元/件的文化衫以50元/件售出，每天可卖200件，在换季时期，预计单价每降低1元，每天可多卖10 件，则销售单价定为多少元时，商店可获利3000元？设销售单价定为x元/件，可列方程.（方程不需化简）

答案解析收藏纠错 + 选题
15. (2021九上·秦淮期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的平分线交弧ACB于点D，则AD的长是.

答案解析收藏纠错 + 选题
16. (2021九上·秦淮期末) 已知 $\text{[math]}$ ，C是平面内一个动点， $\text{[math]}$ ，则满足条件的点C所在区域的面积是.

答案解析收藏纠错 + 选题

三、解答题

17. (2022九上·鄱阳期中) 解方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2021九上·秦淮期末)
1. （1）解方程 $\text{[math]}$ ；
2. （2）方程 $\text{[math]}$ 的解为.
答案解析收藏纠错 + 选题
19. (2021九上·秦淮期末) 已知关于x的方程 $\text{[math]}$ .
1. （1）求证：不论m为何值，该方程都有两个不相等的实数根；
2. （2）若该方程的两个实数根在数轴上所对应的点关于原点对称，则m的值为.
答案解析收藏纠错 + 选题
20. (2021九上·秦淮期末) 如图所示，一块长方形铁皮的长是宽的2倍，四角各截去一个正方形，制成高是5cm，容积是500cm³的无盖长方体容器.求这块铁皮的长和宽.

答案解析收藏纠错 + 选题
21. (2021九上·秦淮期末) 圆周率 $\text{[math]}$ 的故事
我国古代数学家刘徽通过“割圆术”来估计圆周率 $\text{[math]}$ 的值——“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”，可以理解为当正多边形的边数越来越多时，该正多边形与它的外接圆越来越“接近”，这样就可以用正多边形的周长替代它的外接圆的周长，从而估算出圆周率 $\text{[math]}$ 的值.
1. （1）对于边长为a的正方形，其外接圆半径为，根据故事中的方法，用该正方形的周长4a替代它的外接圆周长，利用公式 $\text{[math]}$ ，可以估算 $\text{[math]}$ .
2. （2）类比（1），当正多边形为正六边形时，估计 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
22. (2021九上·秦淮期末) 九年级某班女生进行为期一周的仰卧起坐训练，下面两图是该班女生训练前后“1分钟仰卧起坐”测试的成绩统计图.
1. （1）根据图1提供的信息，补全图2；
2. （2）下列说法正确的是（填写所有正确的序号）
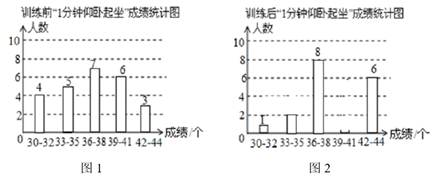
  ①训练前该班女生的平均成绩是 $\text{[math]}$ 个；
  
  ②比较训练前后的成绩，共有3个成绩段的人数变化最大；
  
  ③训练前后成绩的中位数所在的成绩段由“36~38”变为“39~41”.
答案解析收藏纠错 + 选题
23. (2021九上·秦淮期末) 小秋打算去某影城看电影.她用手机打开购票页面，座位已选情况如图所示（虚线边框内为黄金区域，其余为普通区域；深色为已售座位，白色为可选座位）.求下列事件的概率：
1. （1）小秋独自观影，他选择第4排或第5排的概率是；
2. （2）小秋约小叶一同观影，求小秋选择2个同排相邻的座位恰好都在黄金区域的概率.
答案解析收藏纠错 + 选题
24. (2021九上·秦淮期末) 在 $\text{[math]}$ 中， $\text{[math]}$ .
1. （1）如图①，点A在以BC为直径的半圆外，AB、AC分别与半圆交于点D、E，求证： $\text{[math]}$ ；
2. （2）如图②，点A在以BC为直径的半圆内，请用无刻度的直尺在半圆上画出一点D，使得 $\text{[math]}$ 是等腰直角三角形（保留作图痕迹，不写画法）.
答案解析收藏纠错 + 选题
25. (2021九上·秦淮期末) 如图， $\text{[math]}$ 内接于⊙O，过点A作直线AD，使 $\text{[math]}$ .
1. （1）求证：直线AD与⊙O相切.
2. （2）若E是 $\text{[math]}$ 的中点，连接OE并延长交直线AD于点F， $\text{[math]}$ ， $\text{[math]}$ ，则⊙O的半径是.
答案解析收藏纠错 + 选题
26. (2021九上·秦淮期末) 工厂2018年共生产4000万件电子产品，该年还生产了A、B、C三种型号的电池，其数量分别为400万块、800万块、1600万块，这些电池只配装了该年生产的部分电子产品（每一件电子产品配一块电池），剩余电子产品所需电池由其他工厂供给，从2019年起，该工厂逐年扩大这三种类型的电池产量.2019年、2020年这两年，A型电池每年产量的增长率相同，B型电池每年产量的增长率比A型电池每年产量的增长率小1，C型电池每年产量的增长率是A型电池每年产量的增长率的一半，已知该工厂2020年生产的三种类型的电池恰好配装了该年生产的所有电子产品，且该年生产的电子产品的数量是2018年生产的电子产品的数量的3.3倍，求A型电池每年产量的增长率.

答案解析收藏纠错 + 选题
27. (2021九上·秦淮期末) 数学概念
经过初中的数学学习，我们知道图形之间的距离总可以转化为两点之间的距离.一般地，P为图形A上任意一点，Q为图形B上任意一点，则称PQ长的最小值叫做图形A与图形B的距离，记作d（A，B）.
1. （1）概念理解
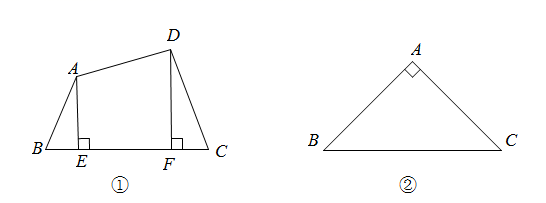
  如图①，在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为E、F，则d（AD，BC）是（）.
  
  A . AB的长 B . AE的长 C . DF的长 D . DC的长
2. （2）知识运用
  如图②，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，P是平面内的一点， $\text{[math]}$ .
  
  ①直接写出d（P，BC）的取值范围；
  
  ②以P为圆心，1为半径作圆，当⊙P在 $\text{[math]}$ 的内部，且与其一边相切时，求⊙P与另两边的距离.
3. （3）问题解决
  如图③，某广场有一个边长为12m的菱形花坛，现准备绕着花坛铺设一条封闭的健身跑道，使靠近花坛的跑道内沿与花坛的距离为2m，则所铺设的健身跑道内沿的长度的最小值为m.
答案解析收藏纠错 + 选题