江苏省盐城市滨海县、建湖县2021届九年级上学期数学期末联考...

更新时间：2021-04-29 浏览次数：145 类型：期末考试

一、单选题

1. (2022七下·皇姑期末) 在4 张相同的卡片上分别写有数1、3、4、6.将卡片的背面朝上并洗匀，从中抽取一张，抽到的数是奇数的概率（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
2. (2021九上·东营月考) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .则下列等式正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·建湖期末) 如图，在 $\text{[math]}$ 中，点D、E、F分别在 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 上，DE∥BC，DF∥AC.下列比例式中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021九上·建湖期末) 两个相似三角形面积比是 $\text{[math]}$ ，其中一个三角形的周长为18，则另一个三角形的周长是（）

A . 12 B . 12或24 C . 27 D . 12或27

答案解析收藏纠错 + 选题
5. (2021九上·建湖期末) 关于x的一元二次方程 $\text{[math]}$ 有实数根，则m取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·建湖期末) 在一场排球比赛中，某排球队6名场上队员的身高（单位： $\text{[math]}$ ）是：180，184，188， 190，192，191，如果用一名身高为 $\text{[math]}$ 的队员替换场上身高为 $\text{[math]}$ 的队员，那么换人后与换人前相比，场上队员身高的平均数和方差大小变化正确的是（）

A . 平均数变小，方差变小 B . 平均数变小，方差变大 C . 平均数变大，方差变大 D . 平均数变大，方差变小

答案解析收藏纠错 + 选题
7. (2021九上·建湖期末) 如图，点E是平行四边形ABCD中BC的延长线上的一点，连接AE交CD于F，交BD于M，则图中共有相似三角形(不含全等的三角形)（）对.

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题

8. (2021九上·建湖期末) 老师给出了二次函数 $\text{[math]}$ 的部分对应值如表：

$\text{[math]}$	…	-3	-2	0	1	3	5	…
$\text{[math]}$	…	7	0	－8	－9	－5	7	…

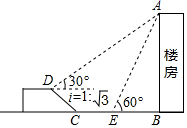
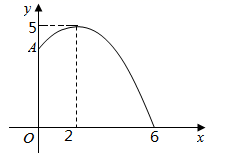
同学们讨论得出了下列结论：①抛物线的开口向上；②抛物线的对称轴为直线 $\text{[math]}$ ；③当 $\text{[math]}$ 时， $\text{[math]}$ ；④ $\text{[math]}$ 是方程 $\text{[math]}$ 的一个根；⑤若 $\text{[math]}$ ， $\text{[math]}$ 是抛物线上从左到右依次分布的两点，则 $\text{[math]}$ .其中正确的是（）

A . ①③④⑤ B . ②③④ C . ①④⑤ D . ③④⑤

答案解析收藏纠错 + 选题

二、填空题

9. (2021九上·建湖期末) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
10. (2021·内江模拟) 一组数据4，4，5，5，x，6，7的平均数是5，则这组数据的中位数是.

答案解析收藏纠错 + 选题
11. (2021九上·建湖期末) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点C、D是 $\text{[math]}$ 两侧 $\text{[math]}$ 上的点，若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2021九上·建湖期末) 如图，经过原点的抛物线是二次函数 $\text{[math]}$ 的图象，那么a的值是.

答案解析收藏纠错 + 选题
13. (2021九上·建湖期末) 小明想测量出电线杆 $\text{[math]}$ 的高度，于是在阳光明媚的星期天，他在电线杆旁的点D处立一标杆 $\text{[math]}$ .使标杆的影子 $\text{[math]}$ 与电线杆的影子 $\text{[math]}$ 部分重叠（即点E、C、A在一直线上）.量得 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米.则电线杆 $\text{[math]}$ 长 $\text{[math]}$ 米.

答案解析收藏纠错 + 选题
14. (2021九上·建湖期末) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的动点，当 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ 相似.

答案解析收藏纠错 + 选题
15. (2021九上·建湖期末) 如图， $\text{[math]}$ 的顶点都是正方形网格中的格点，则 $\text{[math]}$ 等于.

答案解析收藏纠错 + 选题
16. (2021九上·建湖期末) 如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端A点安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为 $\text{[math]}$ 处达到最高，高度为 $\text{[math]}$ ，水柱落地处离池中心距离为 $\text{[math]}$ ，则水管的长度 $\text{[math]}$ 是 $\text{[math]}$ .

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·建湖期末) 求值： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2021九上·建湖期末) 某校组织全校1400名学生进行了“八礼四仪”掌握情况问卷测试.为了解成绩的分布情况，随机抽取了部分学生的成绩（得分取整数.满分为100分），并全制了频数分布表和频数分布直方图（不完整）.

分组

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

合计

频数

20

48

$\text{[math]}$

104

148

400

根据所给信息，回答下列问题：
1. （1）频数分布表中， $\text{[math]}$ .
2. （2）补全频数分布直方图：
3. （3）学校将对分数x在 $\text{[math]}$ 范围内的学生进行奖励，请你估算出全校获奖学生的人数.
答案解析收藏纠错 + 选题
19. (2021九上·建湖期末) 已知关于x的一元二次方程 $\text{[math]}$ .
1. （1）求证：无论m为任意实数，方程总有实数根.
2. （2）如果这个方程的根的判别式的值等于1，求m的值.
答案解析收藏纠错 + 选题
20. (2021九上·建湖期末) 有4张印有“青”、“山”、“绿”、“水”字样的卡片（卡片的开状、大小、质地都相同），放在一个不透明的盒子中，将卡片洗匀.
1. （1）从盒子中任意取出一张卡片，恰好取出印有“青”字的卡片的概率为；
2. （2）先从盒子中任意取出一张卡片，记录后放回并搅匀，再从其中任意取出一张卡片，求取出的两张卡片中，至少有1张印有“青”字的卡片的概率（请画树状图或列表等方法求解）.
答案解析收藏纠错 + 选题
21. (2021九上·建湖期末) 二次函数 $\text{[math]}$ 的图象与y轴交点坐标是 $\text{[math]}$ .
1. （1）求此二次函数解析式；
2. （2）在图中画出二次函数的图象；
3. （3）当 $\text{[math]}$ 时，直接写出y的取值范围为.
答案解析收藏纠错 + 选题
22. (2021九上·建湖期末) 如图，Rt△ABC中，∠ACB=90°，D是BC的中点，CE⊥AD，垂足为E.
1. （1）求证：CD²=DE·AD；
2. （2）求证：∠BED=∠ABC.
答案解析收藏纠错 + 选题
23. (2021九上·建湖期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .求： $\text{[math]}$ 、 $\text{[math]}$ .

答案解析收藏纠错 + 选题
24. (2021九上·建湖期末) 如图，在一次数学综合实践活动中，小亮要测量一教学楼的高度，先在坡面D处测得楼房顶部A的仰角为 $\text{[math]}$ ，沿坡面向下走到坡脚C处，然后向教学楼方向继续行走10米到达E处，测得楼房顶部A的仰角为 $\text{[math]}$ ，已知坡面 $\text{[math]}$ 米，山坡的坡度 $\text{[math]}$ ，求楼房 $\text{[math]}$ 高度（结果精确到0.1米）（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
25. (2023·宜春模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点D在半径 $\text{[math]}$ 上（D与O、A不重合）， $\text{[math]}$ ，且 $\text{[math]}$ .连接 $\text{[math]}$ ，与 $\text{[math]}$ 交于点F，在 $\text{[math]}$ 上取一点E，使 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若D是 $\text{[math]}$ 的中点， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
26. (2021九上·建湖期末) 某商场销售一种小商品，进货价为8元/件.当售价为10元/件时，每天的销售量为100件.在销售过程中发现：销售单价每上涨0.1元，每天的销售量就减少1件.设销售单价为x元/件（ $\text{[math]}$ ），每天销售利润为y元.
1. （1）求y与x的函数关系式；
2. （2）要使每天销售利润不低于270元，求销售单价所在的范围；
3. （3）若每件该小商品的利润不超过 $\text{[math]}$ ，则每件该小商品的销售单价定为多少元时，每天获得的利润最大.最大利润是多少？
答案解析收藏纠错 + 选题
27. (2021九上·建湖期末) 如图，二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ .且与直线 $\text{[math]}$ 相交于坐标轴上的B、C两点.
1. （1）求a、b、c的值；
2. （2）求证： $\text{[math]}$ ；
3. （3）抛物线上是否存在点P，使得 $\text{[math]}$ ？若存在，则求出直线 $\text{[math]}$ 的解析式及P点坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题