 B .
B .  C .
C .  D .
D . 


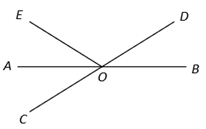
如图,E、F分别在AB和CD上,∠1=∠D,∠2与∠C互余,AF⊥CE于G.
求证:AB CD.
证明:∵AF⊥CE
∴∠CGF=90° ( ▲ )
∵∠1=∠D(已知)
∴ ▲ ▲ ( ▲ )
∴∠4=∠CGF=90°( ▲ )
∵∠2+∠3+∠4=180°(平角的定义)
∴∠2+∠3=90°.
∵∠2与∠C互余(已知),
∴∠2+∠C=90°(互余的定义)
∴∠C=∠3(同角的余角相等)
∴AB CD( ▲ )

收集数据
A.平板支撑 B.跳绳 C.仰卧起坐 D.开合跳 E.其他
通过调查得到的一组数据如下:
DCCADABADB
BEDDEDBCCE
ECBDEEDDED
BBCCDCEDDA
BDDCDDEDCE
整理、描述数据
抽样调查50名初中学生最喜欢的居家体育活动项目人数统计表
|
活动项目 |
划记 |
频数 |
|
A.平板支撑 |
| 4 |
| B.跳绳 |
|
|
| C.仰卧起坐 | 正正 | 10 |
| D.开合跳 |
|
|
| E.其他 | 正正 | 10 |
| 总计 | 50 |

根据以上信息,回答下列问题:
彤彤遇到这样一个问题:
已知:如图甲,AB CD,E为AB,CD之间一点,连接BE,DE,得到∠BED.
求证:∠BED=∠B+∠D.
彤彤是这样做的:
过点E作EF AB,
则有∠BEF=∠B.
∵AB CD,
∴EF CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
请你参考彤彤思考问题的方法,解决问题:如图乙.
已知:直线a b,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.

每年的4月23日是世界读书日.某校为响应“全民阅读”的号召,计划购入A,B两种规格的书柜用于放置图书.经市场调查发现,若购买A种书柜3个、B种书柜2个,共需资金1020元;若购买A种书柜5个、B种书柜3个,共需资金1620元.
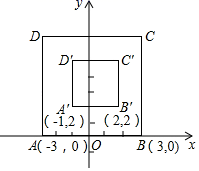
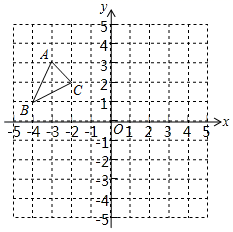
将点P(x,y)平移到P'(x+t,y﹣t)称为将点P进行“t型平移”,点P'称为将点P进行“t型平移”的对应点;将图形G上的所有点进行“t型平移”称为将图形G进行“t型平移”.例如,将点P(x,y)平移到P'(x+1,y﹣1)称为将点P进行“l型平移”,将点P(x,y)平移到P'(x﹣1,y+1)称为将点P进行“﹣l型平移”.
已知点A (2,1)和点B (4,1).

②若线段AB进行“t型平移”后与坐标轴有公共点,则t的取值范围是.