江苏省南通市崇川区启秀中学2021届九年级下学期数学第一次月...

更新时间：2024-07-13 浏览次数：169 类型：月考试卷

一、单选题

1. 实数﹣5的相反数是（）

A . ﹣5 B . $\text{[math]}$ C . ﹣ $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
2. (2021九下·崇川月考) 下列计算中，正确的是（）

A . 2x+5y=7xy B . （x-3）²=x²-9 C . （xy）²=xy² D . （x²）³=x⁶

答案解析收藏纠错 + 选题
3. (2021九下·崇川月考)
如图，直线a⊥直线c，直线b⊥直线c，若∠1=70°，则∠2=（　　）

A . 70° B . 90° C . 110° D . 80°

答案解析收藏纠错 + 选题
4. (2021九下·崇川月考) 下面四个几何体中，俯视图是四边形的几何体共有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2023九上·贵州期末) 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（　　）

A . 戴口罩讲卫生 B . 勤洗手勤通风 C . 有症状早就医 D . 少出门少聚集

答案解析收藏纠错 + 选题
6. (2023九上·渠县期中) 已知关于x 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则m的取值范围是（）

A . m＞－1 B . m＜－2 C . m ≥0 D . m＜0

答案解析收藏纠错 + 选题
7. (2021九下·崇川月考) 如图，△ABC的三个顶点均在格点上，则cosA的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九下·崇川月考) 已知二次函数y=a（x﹣2）²+c（a＞0），当自变量x分别取 $\text{[math]}$ 、3、0时，对应的函数值分别为y₁、y₂、y₃ ，则y₁、y₂、y₃的大小关系是（）

A . y₁＞y₂＞y₃ B . y₂＞y₁＞y₃ C . y₃＞y₁＞y₂ D . y₃＞y₂＞y₁

答案解析收藏纠错 + 选题
9. (2021九下·崇川月考) 如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=﹣ $\text{[math]}$ 的图象上，若点A的坐标为（﹣2，﹣2），则k的值为（）

A . 4 B . ﹣4 C . 8 D . ﹣8

答案解析收藏纠错 + 选题
10. (2022·锡山模拟) 如图，已知A，B两点的坐标分别为（8，0），（0，8），点C，F分别是直线x＝﹣5和x轴上的动点，CF＝10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取得最小值时，sin∠BAD的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021九下·崇川月考) 2020年南通GDP总量突破万亿约为10036亿元，用科学记数法表示为亿元.

答案解析收藏纠错 + 选题
12. (2024八上·昆明期中) 分解因式：3a²﹣12=．

答案解析收藏纠错 + 选题
13. (2020九上·松北期末) 函数 $\text{[math]}$ 中自变量 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
14. (2021九下·崇川月考) 如图，已知AB=AC，DE垂直平分AB分别交AB.AC于D.E两点，若∠A=40°，则∠EBC=°.

答案解析收藏纠错 + 选题
15. (2021九下·崇川月考) 如图，小正方形的边长均为1，扇形OAB是某圆锥的侧面展开图，则这个圆锥的底面周长为.（结果保留π）

答案解析收藏纠错 + 选题
16. (2021九下·崇川月考) 如图，在Rt△ABC中，∠C＝90°，AB＝6，AD是∠BAC的平分线，经过A，D两点的圆的圆心O恰好落在AB上，⊙O分别与AB、AC相交于点E、F.若圆半径为2，则阴影部分面积＝.

答案解析收藏纠错 + 选题
17. (2021九下·崇川月考) 如图，点A在双曲线 $\text{[math]}$ 上，点B在双曲线 $\text{[math]}$ 上，且 $\text{[math]}$ 轴，C、D在x轴上，若四边形ABCD为平行四边形，则它的面积为.

答案解析收藏纠错 + 选题
18. (2021九下·崇川月考) 如图，在平面直角坐标系中，直线l： $\text{[math]}$ 与坐标轴分别交于A，B两点，点C在x正半轴上，且OC＝OB.点P为线段AB（不含端点）上一动点，将线段OP绕点O顺时针旋转90°得线段OQ，连接CQ，则线段CQ的最小值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021九下·崇川月考)
1. （1）计算： $\text{[math]}$ .
2. （2）先化简 $\text{[math]}$ ÷（a＋1）＋ $\text{[math]}$ ，然后a在﹣1、1、2三个数中任选一个合适的数代入求值.
答案解析收藏纠错 + 选题
20. (2021九下·崇川月考) 某校九年级（1）班所有学生参加2010年初中毕业生升学体育测试，根据测试评分标准，将他们的成绩进行统计后分为A、B、C、D四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：
1. （1）九年级（1）班参加体育测试的学生有人；
2. （2）将条形统计图补充完整；
3. （3）在扇形统计图中，等级B部分所占的百分比是，等级C对应的圆心角的度数为°；
4. （4）若该校九年级学生共有850人参加体育测试，估计达到A级和B级的学生共有人.
答案解析收藏纠错 + 选题
21. (2021九下·崇川月考) 一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同。
1. （1）求摸出1个球是白球的概率；
2. （2）摸出1个球，记下颜色后放回，并搅均，再摸出1个球。求两次摸出的球恰好颜色不同的概率（要求画树状图或列表）；
3. （3）现再将n个白球放入布袋，搅均后，使摸出1个球是白球的概率为 $\text{[math]}$ 。求n的值。
答案解析收藏纠错 + 选题
22. (2021·厦门模拟) 如图，在△ABC中，AB=AC，点P在BC上．
1. （1）求作：△PCD，使点D在AC上，且△PCD∽△ABP；(要求：尺规作图，保留作图痕迹，不写作法)
2. （2）在(1)的条件下，若∠APC=2∠ABC，求证：PD//AB．
答案解析收藏纠错 + 选题
23. (2021九下·崇川月考) 如图， $\text{[math]}$ 的对角线 $\text{[math]}$ 交于点E，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 经过点E，与 $\text{[math]}$ 交于点F，G是 $\text{[math]}$ 延长线上一点，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点H，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的直径.
答案解析收藏纠错 + 选题
24. (2021九下·崇川月考) 小张骑自行车匀速从甲地到乙地，在途中因故停留了一段时间后，仍按原速骑行，小李骑摩托车比小张晚出发一段时间，以800米/分的速度匀速从乙地到甲地，两人距离乙地的路程y（米）与小张出发后的时间x（分）之间的函数图象如图所示.
1. （1）求小张骑自行车的速度；
2. （2）求小张停留后再出发时y与x之间的函数表达式；
3. （3）求小张与小李相遇时x的值.
答案解析收藏纠错 + 选题
25. (2021九下·崇川月考) 抛物线y＝﹣x²＋2x＋3与x轴相交于A、B两点，A在B左，与y轴交于点C，顶点为D，抛物线的对称轴DF与BC相交于点E，与x轴相交于点F.
1. （1）求线段DE的长；
2. （2）设过E的直线与抛物线相交于点M（x₁ ， y₁），N（x₂ ， y₂），试判断当|y₁﹣y₂|的值最小时，线段MN的长；
3. （3）在抛物线对称轴上是否存在一点P，使得∠OPB＝135°，若存在，直接写出P点坐标；若不存在，说明理由.
答案解析收藏纠错 + 选题
26. (2021九下·崇川月考) 平面直角坐标系xOy中，对于任意的三个点A、B、C，给出如下定义：若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的“三点矩形”.在点A，B，C的所有“三点矩形”中，若存在面积最小的矩形，则称该矩形为点A，B，C的“最佳三点矩形”.
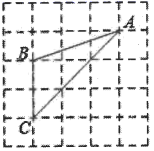
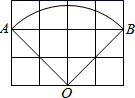
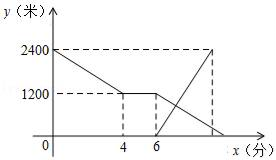
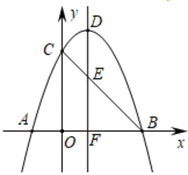
如图1，矩形DEFG，矩形IJCH都是点A，B，C的“三点矩形”，矩形IJCH是点A，B，C的“最佳三点矩形”.

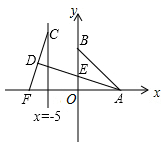
如图2，已知M（4，1），N（﹣2，3），点P（m，n）.
1. （1） ①若m＝1，n＝4，求点M，N，P的“最佳三点矩形”的周长和面积；
  ②若m＝1，点M，N，P的“最佳三点矩形”的面积为24，求n的值；
2. （2）若点P在直线y＝﹣2x+4上.
  ①求点M，N，P的“最佳三点矩形”面积的最小值及此时m的取值范围；
  
  ②当点M，N，P的“最佳三点矩形”为正方形时，求点P的坐标；
3. （3）若点P（m，n）在抛物线y＝ax²+bx+c上，且当点M，N，P的“最佳三点矩形”面积为12时，﹣2≤m≤﹣1或1≤m≤3，直接写出抛物线的解析式.
答案解析收藏纠错 + 选题