
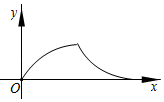
 B .
B . 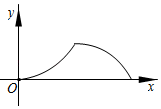 C .
C . 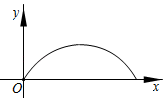 D .
D . 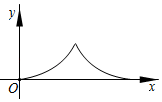


第二小组随机调查了全校三个年级中的100名学生,但只收集到90名学生的有效问卷调查表.
两个小组的调查结果如图的图表所示:
第二小组统计表
|
等级 |
人数 |
百分比 |
|
A |
17 |
18.9% |
|
B |
38 |
42.2% |
|
C |
28 |
31.1% |
|
D |
7 |
7.8% |
|
合计 |
90 |
100% |

若该校共有1000名学生,试根据以上信息解答下列问题:
