 B .
B .  C .
C . 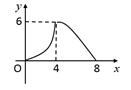 D .
D . 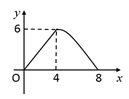
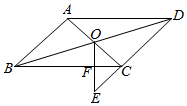

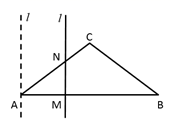
②若 ,求证:四边形AMDN是菱形.
|
销售时段 |
销售数量 |
销售额 |
|
|
A种型号 |
B种型号 |
||
|
第一天 |
300只 |
500只 |
2100元 |
|
第二天 |
400只 |
1000只 |
3800元 |
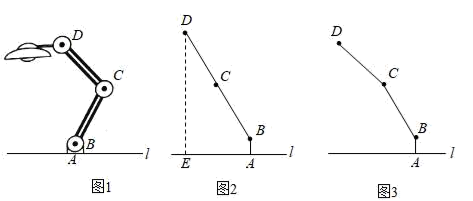
①如图a,当点D在边 上时,请直接写出
与
的数量关系是 ▲ , 线段
与线段
的数量关系是 ▲ ;
②如图b,当点D在边 上时,①中线段
与线段
的数量关系是否成立?若成立,请给予证明;若不成立,请说明理由.