 C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
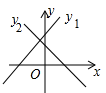 B .
B . 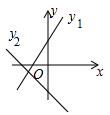 C .
C . 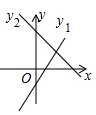 D .
D . 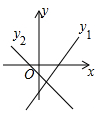
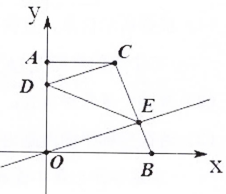

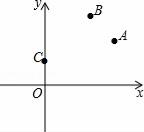


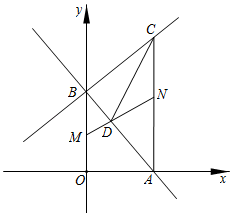
②若(1)中的函数图象和y=-2x+n的函数图象的交点在第一象限,求n的取值范围.
|
销售时段 |
销售数量 |
销售利润 |
|
|
A型 |
B型 |
||
|
第一周 |
3台 |
5台 |
1800元 |
|
第二周 |
4台 |
10台 |
3000元 |
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?

|
运往地 车 型 |
甲 地(元/辆) |
乙 地(元/辆) |
|
大货车 |
720 |
800 |
|
小货车 |
500 |
650 |

②请求出a的值;
①直接写出b的值为 ▲ ;
②求点P的坐标.