一、单项选择题(本大题共8小题,每小题5分,共计40分.)
-
-
A . -2
B . -4
C . 4
D . 2
-
3.
(2021高二下·广州期中)
欧拉恒等式:

被数学家们惊叹为“上帝创造的等式”.该等式将数学中几个重要的数:自然对数的底数

、圆周率

、虚数单位

、自然数1和0完美地结合在一起,它是在欧拉公式:

中,令

得到的.根据欧拉公式,

复平面内对应的点在( ).
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
4.
(2021高二下·大荔期末)
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”,如图是在“赵爽弦图”的基础上创作出的一个“数学风车”,其中正方形ABCD内部为“赵爽弦图”,正方形ABCD外部四个阴影部分的三角形称为“风叶”.现从该“数学风车”的8个顶点中任取2个顶点,则2个顶点取自同一片“风叶”的概率为( ).

-
5.
(2021高二下·广州期中)
在平面直角坐标系

中,已知圆

:

,若直线

:

上有且只有一个点

满足:过点

作圆C的两条切线PM,PN,切点分别为M,N,且使得四边形PMCN为正方形,则正实数m的值为( )
A . 1
B .  C . 3
D . 7
C . 3
D . 7
-
A . 0
B . 35
C . 70
D . -70
-
7.
(2021高二下·思明期中)
我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难人微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数

的图象大致为( ).
-
二、多项选择题(本题共4小题,每小题5分,共20分.)
-
A . 若  、
、  互为异面直线,
互为异面直线,  ,
,  ,
,  ,
,  ,则
,则  B . 若
B . 若  ,
,  ,
,  ,则
,则  C . 若
C . 若  ,
,  ,则
,则  D . 若
D . 若  ,
,  ,
,  ,则
,则 
-
A . 若  ,则
,则  B . 若
B . 若  ,则
,则  C . 若
C . 若  取得最大值时,则
取得最大值时,则  D .
D .  的最大值为
的最大值为 
-
-
A .  可能与平面
可能与平面  平行
B .
平行
B .  与
与  所成的最大角为
所成的最大角为  C .
C .  与
与  一定垂直
D .
一定垂直
D .  与
与  所成的最大角的正切值为
所成的最大角的正切值为 
三、填空题(本大题共4小题,每小题5分,共计20分.)
-
-
-
-
16.
(2021高二下·广州期中)
已知双曲线

的左焦点为

,

为双曲线上一点,

与双曲线

的渐近线平行,且

,其中

为坐标原点,则双曲线

的离心率

.
四、解答题(本大题共6小题,共计70分.)
-
17.
(2021高二下·广州期中)
某市某街道办为了绿植街道两边的绿化带,购进了1000株树苗.这批树苗最矮2米,最高2.5米,桉树苗高度绘制成如图频率分布直方图(如图).
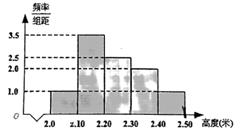
-
-
(2)
现按分层抽样方法.从高度在

的树苗中任取6株树苗.从这6株树苗中任选3株,求3株树苗中至少有一株树苗高度在

的概率.
-
18.
(2023高三上·南京期中)
已知函数

只能同时满足以下三个条件中的两个.
①函数f(x)的最大值是2;
②函数f(x)的图象可由函数  左右平移得到;
左右平移得到;
③函数f(x)的对称中心与f(x)的对称轴之间的最短距离是  .
.
-
(1)
写出这两个条件的序号(不必说明理由)并求出函数

的单调递增区间;
-
(2)
已知

的内角A、B、C所对的边分别为

、

、

,满足

,点

为

的中点,且

,求

的值.
-
-
(1)
证明数列

是等差数列,并求数列

,

的通项公式;
-
(2)
设

,求

.
-
-
(1)
求证:

平面

;
-
(2)
求二面角

的余弦值.
-
21.
(2020高三上·惠州月考)
已知椭圆

的离心率为

,左右顶点分别为

、

,右焦点为

,

为椭圆上异于

、

的动点,且

面积的最大值为

.
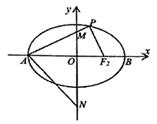
-
(1)
求椭圆

的方程;
-
(2)
设直线

与

轴交于

点,过点

作

的平行线交

轴与点

,试探究是否存在定点

,使得以

为直径的圆恒过定点

.
-
-
(1)
讨论

的单调性;
-

 B .
B .  C .
C .  D .
D . 

左右平移得到;
.