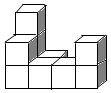
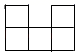
 B .
B .  C .
C . 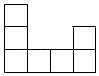 D .
D . 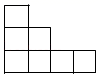
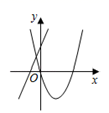 B .
B . 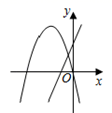 C .
C . 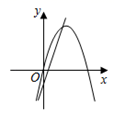 D .
D . 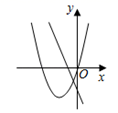
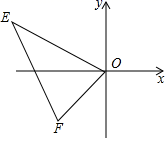
① ;②若
,则
;③对于任意
,始终有
;④若B的坐标为
,则C的坐标为
.
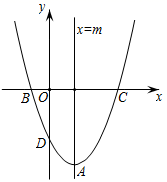
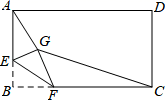
( 1 )关于x的方程x2﹣3x+1=0(x≠0)方程两边同时乘以 得:x-3+
=0即x+
=3,
,
.
( 2 )a3+b3=(a+b)(a2﹣ab+b2);a3﹣b3=(a﹣b)(a2+ab+b2).
根据以上材料,解答下列问题:

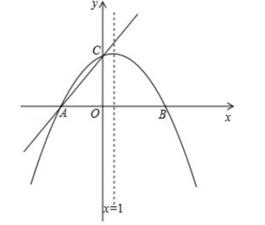
(参考公式:在平面直角坐标之中,若A((x1 , y1),B(x2 , y2),则A,B两点间的距离为AB= )