浙江省备考2021年中考数学模拟试卷（湖州市）

更新时间：2021-05-24 浏览次数：207 类型：中考模拟

一、选择题（本题有10小题，每小题3分，共30分）

1. (2019·夏津模拟) $\text{[math]}$ 的算术平方根是（）

A . 2 B . ±2 C . ± $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 大树的价值很多，可以吸收有毒气体，防止大气污染，增加土壤肥力，涵养水源，为鸟类及其他动物提供繁衍场所等价值，累计计算，一棵50年树龄的大树总计创造价值超过160万元，其中160万元用科学记数法表示为（）

A . 1.6×10⁵ B . 1.6×10⁶ C . 1.6×10⁷ D . 1.6×10⁸

答案解析收藏纠错 + 选题
3. (2020·枣阳模拟) 一个几何体的三视图如图所示，则这个几何体是（）

A . 圆柱 B . 三棱锥 C . 球 D . 圆锥

答案解析收藏纠错 + 选题
4. (2019九上·丹江口期中) 如图，四边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020八上·商河期末) 一组数据4，4，5，5，x，6，7的平均数是5，则这组数据的众数和中位数分别是（）

A . 4，5 B . 4，4 C . 5，4 D . 5，5

答案解析收藏纠错 + 选题
6. (2019·晋宁模拟) 若一次函数y＝kx+b图象经过第一、三、四象限，则关于x的方程x²﹣2x+kb+1＝0的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 只有一个实数根

答案解析收藏纠错 + 选题
7. (2020·平阳模拟) 如图，在菱形 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，以C为圆心、 $\text{[math]}$ 为半径作弧，交 $\text{[math]}$ 于点F，连接 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八下·容县期末) 直线y=－2x+m与直线y=2x－1的交点在第四象限，则m的取值范围是（）

A . m＞－1 B . m＜1 C . －1＜m＜1 D . －1≤m≤1

答案解析收藏纠错 + 选题
9. (2018·嘉兴模拟) 如图，直线l₁∥l₂ ， ⊙O与l₁和l₂分别相切于点A和点B，点M和点N分别是l₁和l₂上的动点，MN沿l₁和l₂平移，若⊙O的半径为1，∠1=60°，下列结论错误的是（）

A . MN= $\text{[math]}$ B . 若MN与⊙O相切，则AM= $\text{[math]}$ C . l₁和l₂的距离为2 D . 若∠MON=90°，则MN与⊙O相切

答案解析收藏纠错 + 选题
10. (2019·瑞安模拟) 如图，小靓用七巧板拼成一幅装饰图，放入长方形ABCD内，装饰图中的三角形顶点E，F分别在边AB，BC上，△GHD的边GD在边AD上，则 $\text{[math]}$ 的值为（　　）

A . $\text{[math]}$ B . 4 $\text{[math]}$ ﹣4 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2023·杨浦模拟) 计算 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2020·百色模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题
13. (2018九上·宜阳期末) 如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD=6，EB=1，则⊙O的半径为．

答案解析收藏纠错 + 选题
14. (2020九上·温州月考) 如图，电路图上有四个开关A、B、C、D和一个小灯泡，在开关全部断开的情况下，闭合其中任意一个开关，灯泡发亮的概率是；若闭合其中任意两个开关，灯泡发亮的概率是.

答案解析收藏纠错 + 选题
15. (2019九上·重庆开学考) 如图，已知M是平行四边形ABCD中AB边的三等分点，BD与CM交于E，则阴影部分面积与平行四边形面积比为.

答案解析收藏纠错 + 选题
16. (2014·北海) 如图，反比例函数y= $\text{[math]}$ （x＞0）的图象交Rt△OAB的斜边OA于点D，交直角边AB于点C，点B在x轴上．若△OAC的面积为5，AD：OD=1：2，则k的值为．

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共66分）

17. (2021·江西模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2020七下·商州期末) 解不等式组 $\text{[math]}$ 并在数轴上画出不等式组的解集．

答案解析收藏纠错 + 选题
19. (2020九下·宁波月考) 图1是一种折叠门，由上下轨道和两扇长宽相等的活页门组成，整个活页门的右轴固定在门框上，通过推动左侧活页门开关。图2是其俯视简化示意图，已知轨道AB=120cm，两扇活页门的宽OC=OB=60cm，点B固定，当点C在AB上左右运动时，OC与OB的长度不变。
1. （1）若∠OBC=53°，求AC的长。
  (结果保留整数，参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3)
2. （2）当点C从点A向右运动60cm时，求点O在此过程中运动的路径长。
答案解析收藏纠错 + 选题
20. (2020·昌吉模拟) 校体育组为了解全校学生“最喜欢的一项球类项目”，随机抽取了部分学生进行调查，下面是根据调查结果绘制的不完整的统计图：

请你根据统计图回答下列问题：
1. （1）喜欢乒乓球的学生所占的百分比是多少？并请补全条形统计图；
2. （2）请你估计全校500名学生中最喜欢“排球”项目的有多少名？
3. （3）在扇形统计图中，“篮球”部分所对应的圆心角是多少度？
4. （4）篮球教练在制定训练计划前，将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈，请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
答案解析收藏纠错 + 选题
21. (2019·咸宁模拟) 如图，OA，OD是⊙O半径．过A作⊙O的切线，交∠AOD的平分线于点C，连接CD，延长AO交⊙O于点E，交CD的延长线于点B．
1. （1）求证：直线CD是⊙O的切线；
2. （2）如果D点是BC的中点，⊙O的半径为 3cm，求 $\text{[math]}$ 的长度．(结果保留π)
答案解析收藏纠错 + 选题
22. (2020九下·无锡期中) 某旅行团32人在景区A游玩，他们由成人、少年和儿童组成．已知儿童10人，成人比少年多12人．
1. （1）求该旅行团中成人与少年分别是多少人?
2. （2）因时间充裕，该团准备让成人和少年（至少各1名）带领10名儿童去另一景区B游玩．景区B的门票价格为100元/张，成人全票，少年8折，儿童6折，一名成人可以免费携带一名儿童．①若由成人8人和少年5人带队，则所需门票的总费用是多少元?②若剩余经费只有1200元可用于购票，在不超额的前提下，最多可以安排成人和少年共多少人带队?求所有满足条件的方案，并指出哪种方案购票费用最少．
答案解析收藏纠错 + 选题
23. (2021九上·南浔期末) 【概念认识】
定义：对角线互相垂直且相等的四边形叫做垂等四边形．
1. （1）如图 1，已知在垂等四边形 ABCD 中，对角线 AC 与 BD 交于点 E ，若 AB⊥AD ， AB＝4cm，cos∠ABD= $\text{[math]}$ 求 AC 的长度，
2. （2）【数学理解】
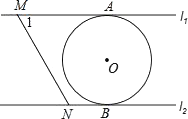
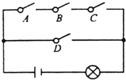
  在探究如何画“圆内接垂等四边形”的活动中，小李与同学讨论出了如下方法：如图 2，在⊙O 中，已知 AB 是⊙O 的弦，只需作 OD⊥OA、OC⊥OB ，分别交⊙O 于点 D 和点 C ，即可得到垂等四边形 ABCD ，请你写出证明过程．
3. （3）【问题解决】
  如图 3，已知 A 是⊙O 上一定点，B 为⊙O 上一动点，以 AB 为一边作出⊙O 的内接垂等四边形(A、B 不重合且 A、B、0 三点不共线)，对角线 AC 与 BD 交于点 E ， ⊙O 的半径为 2 $\text{[math]}$ ，当点 E 到 AD 的距离为 $\text{[math]}$ 时，求弦 AB 的长度．
答案解析收藏纠错 + 选题
24. (2021·余杭模拟) 如图，已知A（-1，0），一次函数 $\text{[math]}$ 的图象交坐标轴于点B、C，二次函数 $\text{[math]}$ 的图象经过点A、C、B.点Q是二次函数图象上一动点。
1. （1）当 $\text{[math]}$ 时，求点Q的坐标；
2. （2）过点Q作直线 $\text{[math]}$ //BC，当直线 $\text{[math]}$ 与二次函数的图象有且只有一个公共点时，求出此时直线 $\text{[math]}$ 对应的一次函数的表达式并求出此时直线 $\text{[math]}$ 与直线BC之间的距离。
答案解析收藏纠错 + 选题