江苏省苏州市2021年中考数学仿真模拟试卷

更新时间：2021-05-27 浏览次数：236 类型：中考模拟

一、选择题

1. (2021·瑞安模拟) 数 $\text{[math]}$ ， $\text{[math]}$ ，3，0中，最大的数是（）

A . $\text{[math]}$ B . π C . 3 D . 0

答案解析收藏纠错 + 选题
2. (2020·徐州模拟) 新型冠状病毒的直径平均为 $\text{[math]}$ ，已知 $\text{[math]}$ ，则 $\text{[math]}$ 用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·娄底模拟) 下列运算正确的是（）

A . （ab）²＝a²b² B . a²+a²＝a⁴ C . （a²）³＝a⁵ D . a²•a³＝a⁶

答案解析收藏纠错 + 选题
4. (2020·云南模拟) 左下图是由四个相同的小立方块搭成的几何体，这个几何体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2019·长春模拟) 若6﹣x＞x，则下列不等式一定成立的是（　　）

A . x≥2 B . x＜3 C . x≥4 D . x≤3

答案解析收藏纠错 + 选题
6. (2020·河南模拟) “十•一”假期，某超市为了吸引顾客，设立了一个转盘游戏进行摇奖活动，并规定顾客每购买200元商品，就获得一次转盘机会，小亮根据摇奖情况制作了一个统计图（如图），请你求出每转动一次转盘获得购物券的平均数是（　　）

A . 43.5元 B . 26元 C . 18元 D . 43元

答案解析收藏纠错 + 选题
7. (2019·长春模拟) 如图，某数学活动小组在吉林广播电视塔周边做数学测算活动、在C处测得最高点A的仰角为α，在D处测得最高点A的仰角为β，点C，B，D在同一条水平直线上，且吉林广播电视塔的高度AB为h（m），则CD之间的距离为（　　）

A . h•（tanα+tanβ）m B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8.
如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD= $\text{[math]}$ ，则阴影部分图形的面积为（　　）

A . 4π B . 2π C . π D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九下·齐齐哈尔期中) 如图，在△ABC中，AB＝2.2，BC＝3.6，∠B＝60°，将△ABC绕点A按逆时针方向旋转得到△ADE，若点B的对应点D恰好落在BC边上时，则CD的长为（）

A . 1.5 B . 1.4 C . 1.3 D . 1.2

答案解析收藏纠错 + 选题
10. (2021九上·黄浦期中) 如图，已知在△ABC纸板中，AC＝4，BC＝8，AB＝11，P是BC上一点，沿过点P的直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么CP长的取值范围是（）

A . 0＜CP≤1 B . 0＜CP≤2 C . 1≤CP＜8 D . 2≤CP＜8

答案解析收藏纠错 + 选题

二、填空题

11. (2020八下·哈尔滨月考) 在函数y= $\text{[math]}$ 中,自变量x的取值范围是.

答案解析收藏纠错 + 选题
12. (2019八上·全椒期中) 已知直线 $\text{[math]}$ ，则将其向右平移1个单位后与两坐标轴围成的三角形的面积为.

答案解析收藏纠错 + 选题
13. (2020九上·台州月考) 如图，把大正方形平均分成9个小正方形，其中有2个小正方形已被涂黑，在剩余的7个白色小正方形中任选一个也涂黑，则使整个涂黑部分成为轴对称图形的概率是．

答案解析收藏纠错 + 选题
14. (2019·长沙模拟) 如图，在⊙O中，CD是直径，弦AB⊥CD ，垂足为E ，连接BC ，若AB＝2 $\text{[math]}$ cm ， ∠BCD＝22°30′，则⊙O的半径为cm ．

答案解析收藏纠错 + 选题
15. (2018·安徽模拟) 若﹣2x^m^﹣ⁿy²与3x⁴y^2m+n是同类项，则m﹣3n的立方根是．

答案解析收藏纠错 + 选题
16. (2020九上·南昌月考) 如图，在 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．将 $\text{[math]}$ 绕点A逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2020·陕西模拟) 如图，在平面直角坐标系中，O为坐标原点，▱ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限.将△AOD沿y轴翻折，使点A落在x轴上的点E处，点B恰好为OE的中点，DE与BC交于点F.若y＝ $\text{[math]}$ （k≠0）图象经过点C，且S_△BEF＝ $\text{[math]}$ ，则k的值为.

答案解析收藏纠错 + 选题
18.
如图，正方形ABCD的边长为1，以AB为直径作半圆，点P是CD中点，BP与半圆交于点Q，连结DQ，给出如下结论：①DQ=1；② $\text{[math]}$ = $\text{[math]}$ ；③S_△PDQ= $\text{[math]}$ ；④cos∠ADQ= $\text{[math]}$ ，其中正确结论是（填写序号）.

答案解析收藏纠错 + 选题

三、解答题

19. (2020九下·吉林月考) 计算 $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2019七下·闵行开学考) 解方程： $\text{[math]}$ + $\text{[math]}$ ＝2

答案解析收藏纠错 + 选题

21. (2020·重庆模拟) 某校对九年级400名学生进行了一次体育测试，并随机抽取甲、乙两个班各50名学生的测试成绩（成绩均为整数，满分50分）进行整理、描述和分析.

下面给岀了部分信息.（用x表示成绩，数据分成5组：A：30≤x＜34，B：34≤x＜38，C：38≤x＜42，D：42≤x＜46，E：46≤x≤50）

乙班成绩在D组的具体分数是：42 42 42 42 42 42 42 42 42 42 43 44 45 45

甲，乙两班成绩统计表：

班级	甲班	乙班
平均分	44.1	44.1
中位数	44.5	n
众数	m	42
方差	7.7	17.4

根据以上信息，回答下列问题：

（1）直接写出m、n的值；
（2）小明这次测试成绩是43分，在班上排名属中游略偏上，小明是甲、乙哪个班级学生？说明理由；
（3）假设该校九年级学生都参加此次测试，成绩达到45分及45分以上为优秀，估计该校本次测试成绩优秀的学生人数.

答案解析收藏纠错 + 选题

22. (2017·浙江模拟) 某人的钱包内有10元钱、20元钱和50元钱的纸币各1张，从中随机取出2张纸币．
1. （1）求取出纸币的总额是30元的概率；
2. （2）求取出纸币的总额可购买一件51元的商品的概率．
答案解析收藏纠错 + 选题
23. (2019七下·江夏期末) 2019年“519（我要走）全国徒步日（江夏站）”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会（活动主办方）为了奖励活动中取得了好成绩的参赛选手，计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元，乙种纪念品每件售价80元.
1. （1）如果购买甲、乙两种纪念品一共花费了9600元，求购买甲、乙两种纪念品各是多少件？
2. （2）设购买甲种纪念品 $\text{[math]}$ 件，如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍，并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案？哪一种方案所需总费用最少？最少总费用是多少元？
答案解析收藏纠错 + 选题
24. (2019九上·淮北期中) 如图，在矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）在（1）的条件下，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
25. (2019九上·通州期末) 已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 形状相同，开口方向不同，其中抛物线 $\text{[math]}$ ： $\text{[math]}$ 交x轴于A，B两点 $\text{[math]}$ 点A在点B的左侧 $\text{[math]}$ ，且 $\text{[math]}$ ，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 交于点A与 $\text{[math]}$ .
1. （1）求抛物线 $\text{[math]}$ ， $\text{[math]}$ 的函数表达式；
2. （2）当x的取值范围是时，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 上的点的纵坐标同时随横坐标的增大而增大；
3. （3）直线 $\text{[math]}$ 轴，分别交x轴， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，P，Q，当 $\text{[math]}$ 时，求线段PQ的最大值.
答案解析收藏纠错 + 选题
26. (2018·丹棱模拟) 问题背景
如图1，等腰△ABC中，AB=AC，∠BAC=120°，作AD⊥BC于点D，则D为BC的中点，
$\text{[math]}$ ，于是 $\text{[math]}$ ．
迁移应用
1. （1）如图2，△ABC和△ADE都是等腰直角三角形，且∠BAC=∠DAE=120°，D，E，C三点在同一直线上，连接BD．
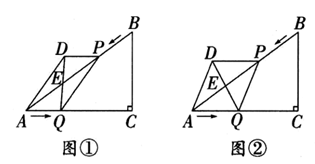
  （ⅰ）求证：△ADB≌△AEC；
  （ⅱ）请直接写出线段AD，BD，CD之间的等量关系式．
2. （2）如图3，在菱形ABCD中，∠ABC=120°，在∠ABC内作射线BM，作点C关于BM的对称点E，连接AE并延长交BM于点F，连接CE，CF．
  （ⅰ）证明：△CEF是等边三角形；
  （ⅱ）若AE=5，CE=2，求BF的长．
答案解析收藏纠错 + 选题
27. (2020九下·无锡月考) 甲，乙两人同时各接受了300个零件的加工任务，甲比乙每小时加工的数量多，两人同时开工，其中一人因机器故障停止加工若干小时后又继续按原速加工，直到他们完成任务。如图表示甲比乙多加工的零件数量y（个）与加工时间x（小时）之间的函数关系，观察图象解决下列问题：
1. （1）其中一人因故障，停止加工小时，C点表示的实际意义是.甲每小时加工的零件数量为个；
2. （2）求线段BC对应的函数关系式和D点坐标；
3. （3）乙在加工的过程中，多少小时时比甲少加工75个零件？
4. （4）为了使乙能与甲同时完成任务，现让丙帮乙加工，直到完成.丙每小时能加工80个零件，并把丙加工的零件数记在乙的名下，问丙应在第多少小时时开始帮助乙？并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
答案解析收藏纠错 + 选题
28. (2020九上·江城月考) 如图①，已知Rt△ABC中，∠C=90°，AC=8cm，BC=6cm，点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2 cm/s。以AQ、PQ为边作四边形AQPD，连接DQ，交AB于点E，设运动的时间为t(单位： s)(0<t≤4)，解答下列问题：
1. （1）用含有t的代数式表示AE=；
2. （2）如图②，当t为何值时，四边形AQPD为菱形；
3. （3）求运动过程中，四边形AQPD的面积的最大值。
答案解析收藏纠错 + 选题