广东省深圳市2021年中考数学五模试卷

更新时间：2022-03-01 浏览次数：133 类型：中考模拟

一、单选题

1. (2024七下·顺德月考) 下列倡导节约的图案中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021九上·历下期末) 下列几何体中，其三视图的三个视图完全相同的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2021·深圳模拟) 在数轴上，点A，B在原点O的两侧，分别表示数a和3，将点A向左平移1个单位长度，得到点C．若 $\text{[math]}$ ，则a的值为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
4. (2021·深圳模拟) 一个多边形的每个内角均为120°，则这个多边形是（　　）

A . 四边形 B . 五边形 C . 六边形 D . 七边形

答案解析收藏纠错 + 选题
5. (2021·深圳模拟) 电影《流浪地球》中，人类计划带着地球一起逃到距地球4光年的半人马星座比邻星．已知光年是天文学中的距离单位，1光年大约是95000亿千米，则4光年约为（　　）

A . 9.5×10⁴亿千米 B . 95×10⁴亿千米 C . 3.8×10⁵亿千米 D . 3.8×10⁴亿千米

答案解析收藏纠错 + 选题
6. (2021·深圳模拟) 如果a﹣b＝ $\text{[math]}$ ，那么代数式 $\text{[math]}$ 的值为（　　）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·深圳模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是等圆， $\text{[math]}$ 内接于 $\text{[math]}$ ，点C ， E分别在 $\text{[math]}$ ， $\text{[math]}$ 上．如图，①以C为圆心， $\text{[math]}$ 长为半径作弧交 $\text{[math]}$ 于点D ，连接 $\text{[math]}$ ；②以E为圆心， $\text{[math]}$ 长为半径作弧交 $\text{[math]}$ 于点F ，连接 $\text{[math]}$ ；下面有四个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，所有正确结论的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2021·深圳模拟) 改革开放40年以来，城乡居民生活水平持续快速提升，居民教育、文化和娱乐消费支出持续增长，已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出，如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图．

说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如2018年第二季度与2017年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如2018年第二季度与2018年第一季度相比较．

根据上述信息，下列结论中错误的是（　　）

A . 2017年第二季度环比有所提高 B . 2017年第三季度环比有所提高 C . 2018年第一季度同比有所提高 D . 2018年第四季度同比有所提高

答案解析收藏纠错 + 选题
9. (2023九上·杭州月考) 已知点A(a－m ， y₁)、B(a－n ， y₂)、C(a+b ， y₃)都在二次函数y=x²－2ax +1的图象上，若0<m<b<n ，则y₁、y₂、y₃的大小关系是（）

A . y₁< y₂< y₃ B . y₁ < y₃< y₂ C . y₃< y₁< y₂ D . y₂< y₃< y₁

答案解析收藏纠错 + 选题
10. (2021·深圳模拟) 如图，一次函数 $\text{[math]}$ 的图象与x轴，y轴交于A ， B两点，与反比例函数 $\text{[math]}$ 的图象相交于C ， D两点，分别过C ， D两点作y轴，x轴的垂线，垂足为E ， F ，连接 $\text{[math]}$ ．有下列四个结论：① $\text{[math]}$ 与 $\text{[math]}$ 的面积相等；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ．其中正确的结论是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·淮安模拟) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是.

答案解析收藏纠错 + 选题
12. (2021·深圳模拟) 如图，在△ABC中，AB=AC=5，BC=8，中线AD、CE相交于点F ，则AF的长为．

答案解析收藏纠错 + 选题
13. (2021·深圳模拟) 如图，已知正方形OABC的三个顶点坐标分别为A (2，0)，B (2，2)，C (0，2)，若反比例函数 $\text{[math]}$ 的图象与正方形OABC的边有交点，请写出一个符合条件的k值．

答案解析收藏纠错 + 选题
14. (2021·深圳模拟) 如图，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 经过点A ， C ， D与 $\text{[math]}$ 交于点E ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2021·深圳模拟) 如图所示的网格是正方形网格，则 $\text{[math]}$ °（点A，B，C，D，E是网格线交点）．

答案解析收藏纠错 + 选题

三、解答题

16. (2022九下·易县模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2021·深圳模拟) 化简： $\text{[math]}$ ，并挑选合适的值代入求值．

答案解析收藏纠错 + 选题
18. (2021·深圳模拟) 某校在宣传“民族团结”活动中，采用四种宣传形式：A．器乐，B．舞蹈，C．朗诵，D．唱歌．每名学生从中选择并且只能选择一种最喜欢的，学校就宣传形式对学生进行了抽样调查，并将调查结果绘制了如下两幅不完整的统计图．

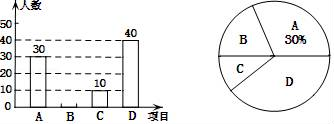
请结合图中所给信息，解答下列问题：
1. （1）本次调查的学生共有人；
2. （2）补全条形统计图；
3. （3）该校共有1200名学生，请估计选择“唱歌”的学生有多少人？
4. （4）七年一班在最喜欢“器乐”的学生中，有甲、乙、丙、丁四位同学表现优秀，现从这四位同学中随机选出两名同学参加学校的器乐队，请用列表或画树状图法求被选取的两人恰好是甲和乙的概率．
答案解析收藏纠错 + 选题
19. (2021九上·茂南期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D是 $\text{[math]}$ 边的中点，连接 $\text{[math]}$ ，分别过点A，C作 $\text{[math]}$ ， $\text{[math]}$ 交于点E，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点O．
1. （1）求证：四边形 $\text{[math]}$ 是矩形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
20. (2021八下·兴庆期末) 某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元．
1. （1）求出A型、B型污水处理设备的单价；
2. （2）经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．
答案解析收藏纠错 + 选题
21. (2021·深圳模拟) 如图1，点E为△ABC边AB上的一点，⊙O为△BCE的外接圆，点D为 $\text{[math]}$ 上任意一点．若AE=AC=2n ， BC=n²－1，BE=n²－2n+1 ．(n≥2，且n为正整数) ．
1. （1）求证：∠CAE+∠CDE=90°；
2. （2） ①如图2，当CD过圆心O时，①将△ACD绕点A顺时针旋转得△AEF ，连接DF ，请补全图形，猜想CD、DE、DF之间的数量关系，并证明你的猜想；②若n=3，求AD的长．
答案解析收藏纠错 + 选题
22. (2021·深圳模拟) 如图，抛物线y=ax²－2ax+c与x轴分别交于点A、B(点B在点A的右侧)，与y轴交于点C ，连接BC ，点( $\text{[math]}$ ， $\text{[math]}$ a－3)在抛物线上．
1. （1）求c的值；
2. （2）已知点D与C关于原点O对称，作射线BD交抛物线于点E ，若BD=DE ， ①求抛物线所对应的函数表达式；②过点B作BF⊥BC交抛物线的对称轴于点F ，以点C为圆心，以 $\text{[math]}$ 的长为半径作⊙C ，点T为⊙C上的一个动点，求 $\text{[math]}$ TB+TF的最小值．
答案解析收藏纠错 + 选题