浙江省宁波市海曙区2021年数学中考模拟试卷（5月）

更新时间：2024-07-13 浏览次数：231 类型：中考模拟

一、单选题

1. (2021·海曙模拟) 数1，0， $\text{[math]}$ ， $\text{[math]}$ 中最大的是（　）

A . 1 B . 0 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021·海曙模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·海曙模拟) 宁波市“十四五”规划中指出，到二〇二五年，经济总量和发展质量跃上新台阶，全市生产总值达到1.7万亿元，其中1.7万亿元用科学记数法表示为（）

A . $\text{[math]}$ 元 B . $\text{[math]}$ 元 C . $\text{[math]}$ 元 D . $\text{[math]}$ 元

答案解析收藏纠错 + 选题
4. (2021·海曙模拟) 能说明命题“当a为实数时，则 $\text{[math]}$ ”是假命题的反例是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·海曙模拟) 如图所示的几何体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2021·海曙模拟) 一组数据1，2，3，4，5的方差是a，若增加一个数据9，则增加后6个数据的方差为b，则a与b的大小关系是（）

A . a < b B . a = b C . a > b D . 不能确定

答案解析收藏纠错 + 选题
7. (2023·鹿城模拟) 如图为一节楼梯的示意图，BC⊥AC，∠BAC=α，AC=6米。现要在楼梯上铺一块地毯，楼梯宽度为1米，则地毯的面积至少需要（）平方米。

A . 6tanα+6 B . $\text{[math]}$ +6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·海曙模拟) 在平面直角坐标系中，点 $\text{[math]}$ ，则点P不可能在（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
9. (2021·海曙模拟) 如图，⊙O经过菱形ABCD的顶点B，C，且与边AD相切于点E.若AE＝1，ED＝5，则⊙O的半径为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九上·六安月考) 如图，在Rt△ABC中，∠BAC=90^° ，以其三边为边分别向外作正方形，延长EC，DB分别交GF，AH于点N，K，连结KN交AG于点M，若S₁-S₂=2，AC=4，则AB的长为（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024·巴中) $\text{[math]}$ 的立方根是．

答案解析收藏纠错 + 选题
12. (2024九下·盱眙模拟) 因式分解： $\text{[math]}$ =.

答案解析收藏纠错 + 选题
13. (2021·海曙模拟) 一张圆形纸片裁剪后正好能做三个一样的无底圆锥纸帽（无余料，接缝不计），若圆锥的高为4cm，则每个圆锥的侧面积是.

答案解析收藏纠错 + 选题

14. (2021·海曙模拟) 为落实省新课改精神，宁波市各校都开设了“知识拓展类”、“体艺特长类”、“实践活动类”三类拓展课程.下列数据是某校八年级学生“体艺特长类”课程的参与情况：

课程（类别）	艺术修养	快乐足球	魅力舞蹈	笔墨载古	美丽瑜伽	精英篮球
人数（人）	20	24	18	23	18	16

则这组数据的中位数为人.

答案解析收藏纠错 + 选题

15. (2021·海曙模拟) 如图，已知在△ABC中，∠C=60°，⊙O是△ABC的外接圆，过点A、B分别作⊙O的切线，两切线交于点P，若⊙O的半径为1，则△PAB的周长为 .

答案解析收藏纠错 + 选题
16. (2021·海曙模拟) 如图，已知双曲线 $\text{[math]}$ 和 $\text{[math]}$ ，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于点A，将直线 $\text{[math]}$ 向下平移与双曲线 $\text{[math]}$ 交于点B，与y轴交于点P，与双曲线 $\text{[math]}$ 交于点C， $\text{[math]}$ ， $\text{[math]}$ ，则k的值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2021·海曙模拟)
1. （1）计算： $\text{[math]}$
2. （2）解方程： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2021·海曙模拟) 如图，∠ACB在6×6方格中，点A，B，C在格点上，按要求画图：
1. （1）在图1中画出∠APB，使得∠APB＝∠ACB，点P为格点.
2. （2）在图2中画出∠AMB，使得∠AMB+∠ACB＝180°，点M为格点.
答案解析收藏纠错 + 选题
19. (2021·海曙模拟) 某校将九年级学生英语人机对话的一次模拟测试成绩分为A，B，C，D四个等级，现随机抽取一部分学生的成绩进行统计，并绘制了下列两幅统计图（部分信息未给出）：
1. （1）求扇形统计图中C等级所对应的圆心角的度数；
2. （2）请将条形统计图补充完整；
3. （3）记A或B等级的成绩为优秀，若该校九年级学生共600人，请你估计成绩为优秀的学生有多少人？
答案解析收藏纠错 + 选题
20. (2021·海曙模拟) 如图1，一扇窗户打开后可以用窗钩AB将其固定，窗钩的一个端点A固定在窗户底边OE上，且与转轴底端O之间的距离为20cm，窗钩的另一个端点B可在窗框边上的滑槽OF上移动，滑槽OF的长度为17cm，AB、BO、AO构成一个三角形．当窗钩端点B与点O之间的距离是7cm的位置时（如图2），窗户打开的角∠AOB的度数为37°．
1. （1）求钩AB的长度（精确到1cm）；
2. （2）现需要将窗户打开的角∠AOB的度数调整到45°时，求此时窗钩端点B与点O之间的距离（精确到1cm）．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75， $\text{[math]}$ ≈1.4）
答案解析收藏纠错 + 选题
21. (2021·海曙模拟) 如图，在Rt△ACB中，∠ACB＝90°，点D为BC延长线上一点，以BD为直径作半圆O分别交AB，AC于点G，E，点E为 $\text{[math]}$ 的中点，过点E作⊙O的切线交AB于点F.
1. （1）求证：∠AEF＝∠ABC.
2. （2）若sinA＝ $\text{[math]}$ ，FG＝1，求AC的长.
答案解析收藏纠错 + 选题
22. (2021·海曙模拟) 某款轿车每行驶100千米的耗油量y升与其行驶速度x千米/小时之间的函数关系图象如图所示，其中线段AB的表达式为 $\text{[math]}$ ，点C的坐标为（140，14），即行驶速度为140千米/小时时该轿车每行驶100千米的耗油量是14升.
1. （1）求线段BC的表达式；
2. （2）如果从甲地到乙地全程为260千米，其中有60千米限速50千米/小时的省道和200千米限速120千米/小时的高速公路，那么在不考虑其他因素的情况下，这款轿车从甲地行驶到乙地至少需要耗油多少升？
答案解析收藏纠错 + 选题
23. (2022九下·海曙开学考) 如果抛物线C₁： $\text{[math]}$ 与抛物线C₂： $\text{[math]}$ 的开口方向相反，顶点相同，我们称抛物线C₂是C₁的“对顶”抛物线.
1. （1）求抛物线 $\text{[math]}$ 的“对顶”抛物线的表达式；
2. （2）将抛物线 $\text{[math]}$ 的“对顶”抛物线沿其对称轴平移，使所得抛物线与原抛物线 $\text{[math]}$ 形成两个交点M、N，记平移前后两抛物线的顶点分别为A、B，当四边形AMBN是正方形时，求正方形AMBN的面积.
3. （3）某同学在探究“对顶”抛物线时发现：如果抛物线C₁与C₂的顶点位于x轴上，那么系数b与d，c与e之间的关系是确定的，请写出它们之间的关系.
答案解析收藏纠错 + 选题
24. (2021·海曙模拟) 如图，在Rt△ABC中，∠ABC=90°，AB=1，AC= $\text{[math]}$ ，点M是线段CA上的动点(M不与点A、C重合)，作△ABM的外接圆⊙O，过点A作AN $\text{[math]}$ BC，交⊙O于N点.
1. （1） tanC的值为.
2. （2）若△ANM∽△CMB(其中点A与点C对应，点M与点B对应)，求AM的长.
3. （3） ①若△AMN为等腰三角形，求线段MC的长度.
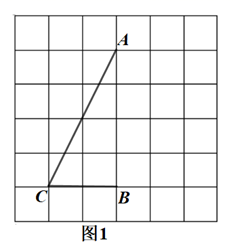
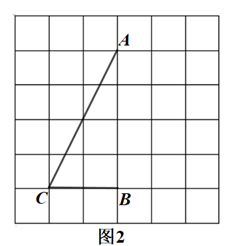
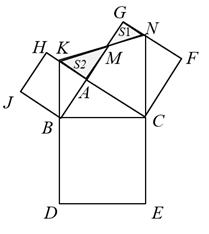
  ②若S_△BMN=S_△BMC ，请直接写出此时△BMN的面积 ▲ .
答案解析收藏纠错 + 选题