贵州省贵阳市云岩区2021年数学中考适应性试卷

更新时间：2021-07-27 浏览次数：182 类型：中考模拟

一、单选题

1. (2021·云岩模拟) 如图，在数轴上标注了①②③④四段范围，则原点 $\text{[math]}$ 位于（）

A . 第①段 B . 第②段 C . 第③段 D . 第④段

答案解析收藏纠错 + 选题
2. (2021·云岩模拟) 如图，直线 $\text{[math]}$ ，通过度量测得 $\text{[math]}$ ， $\text{[math]}$ 之间的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·云岩模拟) 如图，在平面直角坐标系中有一点 $\text{[math]}$ ，点 $\text{[math]}$ 经过平移变换后落在第二象限内，则平移方式是（）

A . 向左平移1个单位长度 B . 向下平移2个单位长度 C . 向左平移4个单位长度 D . 向下平移3个单位长度

答案解析收藏纠错 + 选题
4. (2021·云岩模拟) 数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具，此时测得 $\text{[math]}$ ，对角线 $\text{[math]}$ 长为 $\text{[math]}$ ，改变教具的形状成为图2所示的正方形，则正方形的边长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·云岩模拟) 下面是两位同学在讨论一个一元一次不等式，根据对话提供的信息，他们讨论的不等式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·合肥模拟) 阿基米德说：“给我一个支点，我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理，即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为 $\text{[math]}$ 和 $\text{[math]}$ ，则这一杠杆的动力 $\text{[math]}$ 和动力臂 $\text{[math]}$ 之间的函数图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023八下·广信期末) 2021年是中国共产党建党100周年，某校举行了“党在我心中”的主题演讲比赛.九年级10名同学参加了该演讲比赛，成绩如下表.则这组数据的众数和中位数分别是（）

成绩/分

80

85

90

95

人数/人

2

3

4

1

A . 85分，85分 B . 90分，90分 C . 90分，85分 D . 90分，87.5分

答案解析收藏纠错 + 选题
8. (2021九上·长丰期末) 如图， $\text{[math]}$ 的顶点位于正方形网格的格点上，若 $\text{[math]}$ ，则满足条件的 $\text{[math]}$ 是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2021·云岩模拟) 利用尺规作一个任意三角形的内心 $\text{[math]}$ ，以下作法正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2021·云岩模拟) 图2是由图1的窗户抽象出来的平面图形，半圆的直径与长方形的宽相等，此平面图形的对称轴与半圆的直径将图形分成四个部分，半圆的圆心点 $\text{[math]}$ 处有一任意转动指针，指针停止的位置是等可能的，则指针指向阴影部分的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 因为长方形的长未知，所以概率不确定

答案解析收藏纠错 + 选题
11. (2021·云岩模拟) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ 是一元一次方程，则方程的解为（）

A . -2 B . 2 C . -6 D . -1

答案解析收藏纠错 + 选题
12. (2021·云岩模拟) 若二次函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为常数， $\text{[math]}$ ）的图象上有五个不同的点： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2024八上·肇源月考) $\text{[math]}$ 的立方根是．

答案解析收藏纠错 + 选题
14. (2021·云岩模拟) 如图，小莉用灯泡 $\text{[math]}$ 照射一个矩形硬纸片 $\text{[math]}$ ，在墙上形成矩形影子 $\text{[math]}$ ，现测得 $\text{[math]}$ ， $\text{[math]}$ ，纸片 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则影子 $\text{[math]}$ 的面积为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2021·云岩模拟) 一次函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 为常数， $\text{[math]}$ ）的图象如图所示，当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
16. (2022九下·安顺月考) 如图，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将矩形 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转得到矩形 $\text{[math]}$ ，边 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题

三、解答题

17. (2021·云岩模拟) 为“弘扬美食文化，助力黔菜出山”，某数学兴趣小组在云岩广场随机抽取500位云岩区市民填写了“舌尖上的贵阳——我最喜爱的贵阳小吃”调查问卷，兴趣小组将调查问卷整理后绘制成如下统计图，请根据所给信息解答以下问题：
1. （1）请补全条形统计图；
2. （2）已知云岩区人口约100万人，请估计云岩区市民中最喜欢“老素粉”的有多少万人？
3. （3） “五·一”小长假期间，来筑旅游的小度要从以上四种小吃中随机选择两种不同的小吃进行品尝，请用列表或画树状图的方法，求他选中“肠旺面”和“豆腐果”的概率.
答案解析收藏纠错 + 选题
18. (2021·云岩模拟) 同学们，你们知道吗？三角形的内角和不一定是180°.
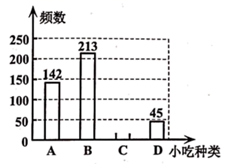
德国数学家黎曼创立的黎曼几何中描述：在球面上选三个点连线构成一个三角形，这个三角形的内角和大于180°.黎曼几何开创了几何学的新领域，近代黎曼几何在广义相对论里有着重要的应用.同样，在俄国数学家罗巴切夫斯基发表的新几何（简称罗氏几何）中，描述了在双曲面里画出的三角形，它的内角和永远小于180°.罗氏几何在天体理论中有着广泛的应用.而我们所学习的欧氏几何中描述“在平面内，三角形的内角和等于180°”是源于古希腊数学家欧几里得编写的《原本》.欧几里得创造的公理化体系影响了世界2000多年，是整个人类文明史上的里程碑.

请你证明：在平面内，三角形的内角和等于180°.要求画出图形，写出已知、求证和证明.

答案解析收藏纠错 + 选题
19. (2021·云岩模拟) 如下表，从左到右在每个格子中都填入了一个整数，使得其中任意三个相邻格子中所填的整数之和都相等.

-1

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

5

-2

…
1. （1）格子中 $\text{[math]}$ 所表示的整数为， $\text{[math]}$ 所表示的整数为， $\text{[math]}$ 所表示的整数为；
2. （2）请你求出第2021个整数是多少？
答案解析收藏纠错 + 选题
20. (2021·云岩模拟) 如图1，用平面去截一个正方体，得到了一个如图2的几何体，通过测量得到 $\text{[math]}$ ， $\text{[math]}$ .

（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
21. (2021·云岩模拟) 如图， $\text{[math]}$ 的顶点 $\text{[math]}$ 在原点上，顶点 $\text{[math]}$ ， $\text{[math]}$ 分别在反比例函数 $\text{[math]}$ （ $\text{[math]}$ 为常数， $\text{[math]}$ ， $\text{[math]}$ ）， $\text{[math]}$ $\text{[math]}$ 的图象上，对角线 $\text{[math]}$ 轴于 $\text{[math]}$ ，已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .
1. （1）求点 $\text{[math]}$ 的坐标；
2. （2）若 $\text{[math]}$ 的面积是12，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
22. (2021·云岩模拟) 如图，正方形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 上的一点，连接 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的度数；
2. （2）当点 $\text{[math]}$ 为 $\text{[math]}$ 的中点时， $\text{[math]}$ 是 $\text{[math]}$ 的内接正 $\text{[math]}$ 边形的一边，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
23. (2021八上·如皋月考) 我区在一项工程招标时，接到甲、乙两个工程队的投标书，从投标书中得知有三种方案.
A方案：甲队单独完成这项工程，刚好如期完成；

B方案：乙队单独完成这项工程需要的时间是规定时间的2倍；

C方案：**********，剩下的工程由乙队单独做，也正好如期完成.

已知，一个同学按照C方案，设规定的工期为 $\text{[math]}$ 天，

根据题意列出方程： $\text{[math]}$ .
1. （1）根据所列方程，C方案中“**********”部分描述的已知条件应该是：；
2. （2）从投标书中得知，甲工程队每施工一天所需费用1.1万元，乙工程队每施工一天所需费用0.5万元，请你在如期完成的两种方案中，判断哪种方案更省钱，说明理由.
答案解析收藏纠错 + 选题
24. (2021·云岩模拟) 新定义：有三个内角相等的四边形叫做三等角四边形.
1. （1）在三等角四边形 $\text{[math]}$ 中， $\text{[math]}$ ，那么 $\text{[math]}$ °；
2. （2）如图1，折叠平行四边形纸片 $\text{[math]}$ ，使顶点 $\text{[math]}$ ， $\text{[math]}$ 分别落在边 $\text{[math]}$ ， $\text{[math]}$ 上的点 $\text{[math]}$ ， $\text{[math]}$ 处，折痕分别为 $\text{[math]}$ ， $\text{[math]}$ .求证：四边形 $\text{[math]}$ 是三等角四边形；
3. （3）如图2，在三等角四边形 $\text{[math]}$ 中， $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
25. (2021·云岩模拟) 如图，已知一次函数 $\text{[math]}$ 的图象分别与 $\text{[math]}$ 轴 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ ，在二次函数 $\text{[math]}$ 中， $\text{[math]}$ 是一个不为0的常数.
1. （1）若二次函数的图象过点 $\text{[math]}$ ，则 $\text{[math]}$ 的值是；
2. （2）点 $\text{[math]}$ 是二次函数图象的顶点，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）二次函数的图象与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ .能使 $\text{[math]}$ 与坐标轴所成的夹角等于 $\text{[math]}$ 的 $\text{[math]}$ 有几个？请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题